All published articles of this journal are available on ScienceDirect.
Kappa Statistics: A Method of Measuring Agreement in Dental Examinations
Abstract
Statistical methods have always been the solution to medical problems. Due to the problem of inconsistency in the diagnosis of dentists, statistical science has been provided for measuring the compatibility of diagnosis and reliability of dentists. One of the most important statistical methods for examining the agreement between the two experiments or diagnoses is Kappa statistics which can be used in dental sciences. The present study reviewed different types of Kappa statistics for assessing agreement, including Cohen's kappa, Fleiss' kappa, and Cohen's weighted kappa.
1. INTRODUCTION
Dentistry is one of the sciences in that direct observation of the doctor and his personal opinion during the examination has a direct effect on the final diagnoses [1]. Due to the multiplicity of dentists, the Decayed Missing Filled (DMF) Index was introduced to integrate diagnoses and standardize diagnostic criteria in the field of caries [2]. However, later it became clear that the accuracy of the index is not a guarantee for the consistency of dentists' diagnosis. Even a dentist can make a heterogeneous diagnosis on two examinations. Factors such as prior knowledge, experience, and aptitude directly affect dentists' diagnoses.
Statistical methods can always be used to solve medical problems. Considering the fact that there is inconsistency in dental diagnosis, which both the World Health Organization and the International Dental Federation are concerned about, statistics is an indicator for measuring the consistency of diagnoses in dental examinations [3]. One of the most widely used statistical methods to check the agreement between two diagnoses used in dental sciences is the Kappa statistic. To the best of our knowledge, there were no tutorial studies that mention all types of Kappa statistics and applications in dentistry. So this tutorial study aimed to introduce all types of Kappa statistics and their application in dental science in a simple way for dummies. Different types of Kappa and their applications for measuring agreement in dentistry are presented with examples in the following sections.
2. DIFFERENT TYPES OF KAPPA STATISTICS
2.1. Cohen's Kappa
Cohen's kappa (CK) was introduced by Jacob Cohen in 1960 and is often used to assess concordance between two raters [4]. CK is a statistic that is used to measure inter-rater reliability for qualitative items. Also, it is generally thought to be a more robust measure than a simple percent agreement calculation [5, 6]. In dentistry, this index can be defined as follows:
Suppose two dentists examine the same tooth, the rate of concordance in their diagnoses can be measured in the form of a statistical index called kappa. It requires the final diagnosis of each dentist to be a dichotomous variable, such as a healthy or decayed tooth. Accordingly, a table with two rows for the first diagnosis and two columns for the second diagnosis is made as a 2 × 2 table such as the one represented in Table 1.
After creating a 2 x 2 table, Cohen's kappa (CK) uses the numbers in the table to evaluate the agreement of two dentists in examining patients and diagnosing decayed teeth [7]. To define this statistic, we first need to introduce the observed proportion of agreement and expected probability (Table 1).
2.1.1. Raw Agreement (P0)
In Table 1, agreement between the two dentists is represented in cells A and D, so calculating the raw agreement can be done as follows: (Eq 1).
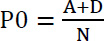 [8], [8],
|
(1) |
2.1.2. The Expected Agreement (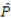 )
)
To calculate the expected agreement (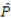 ), in each row and column, the sum of rows and columns is calculated, then the sum of the first row is multiplied by the sum of the first column and the sum of the second column is also multiplied by the sum of the second row. The resulting products are added together and divided by the square of the sample size. Below is the formula for calculating the expected agreement and Cohen's kappa: (Eq 2)
), in each row and column, the sum of rows and columns is calculated, then the sum of the first row is multiplied by the sum of the first column and the sum of the second column is also multiplied by the sum of the second row. The resulting products are added together and divided by the square of the sample size. Below is the formula for calculating the expected agreement and Cohen's kappa: (Eq 2)
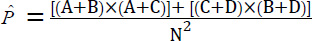 [9] [9]
|
(2) |
N= total sample size
Now, one can define kappa statistics using the formulae presented in sections I and II as follows: (Eq 3).
| - | - | The Diagnosis of Dentist 2 | |
|---|---|---|---|
| - | - | Healthy Tooth | Decayed Tooth |
| The diagnosis of Dentist 1 | Healthy Tooth | A | B |
| Decayed Tooth | C | D | |
The range of values for Kappa statistics is between -1 to 1 [12, 13]. If the values are less than zero, it indicates no agreement, values between 0.6 and 0.8 indicate moderate agreement and values greater than 0.8 mean nearly complete agreement [9]. A generalized form of Cohen's kappa statistic for more than two raters was introduced by Fleiss in 1970, known as Fleiss's kappa [7, 13].
Example 1: Suppose two dentists examine 100 teeth (N=100) at the end of a working day so both of them diagnose 40 decayed and 30 healthy teeth. Then, the first dentist will diagnose 20 cases of them as rotten, while the second dentist will diagnose them as healthy. Also if dentist 1 diagnoses 10 cases as healthy while the second dentist has diagnosed them as decayed at the same time, the data are given in the 2 × 2 table as follows (Table 2).
| - | - | The Diagnosis of Dentist 2 | |
|---|---|---|---|
| - | - | Healthy Tooth | Decayed Tooth |
| The diagnosis of Dentist 1 | Healthy Tooth | 40 | 10 |
| Decayed Tooth | 20 | 30 | |
For our example in Table 2, the raw agreement in diagnosis between the two dentists is 0.7.
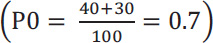
So, for our example in Table 2, its value is 0.46.
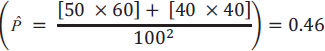
Therefore, in our example in Table 2, the kappa statistic is equal to 0.44.
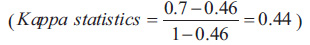 , it shows the agreement between to dentist is low.
, it shows the agreement between to dentist is low.
2.2. Fleiss' Kappa
Fleiss' kappa was introduced by Fleiss et al. between 1970 and 2003 [14]. This index is used to check the agreement of the results diagnosed by two or more evaluators. It is necessary for the diagnosis result to be a qualitative variable (good or bad, sick or healthy, normal or moderate or severe) [15, 16].
In calculating Fleiss' kappa, one must first create a table where each row of the table corresponds to a patient and the columns represent the possible categorical scores so that there is one column for each score. The values in the cells of the table reflect the number of raters (dentists in the previous example) who chose that score (nij). Then a probability is calculated for the row and column according to the following relations. Row probabilities for each patient are calculated from (Eq. 4) and column probabilities are calculated from equation (Eq. 6). Then, the raw agreement probability is calculated based mean of raw probabilities (Pi) as (Eq. 5). The amount of expected agreement is also calculated through relation. Finally, like the previous formula that we had in Cohen's kappa, the calculations are obtained (Table 3).
Fleiss kappa is not a multi-rater extension of Cohen's kappa [17].
| - | Range of Categorical Score (K) | - | ||||||
|---|---|---|---|---|---|---|---|---|
| Patients (N) | 1 | 2 | 3 | 4 | … | Pi | ||
| Patient 1 | n11 | n12 | n13 | n14 | - | - | ||
| Patient 2 | n21 | n22 | n23 | n24 | - | - | ||
| …. | - | - | - | - | nij | - | ||
| Pj | - | - | - | - | - | - | ||
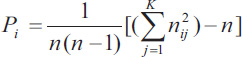 |
(4) |
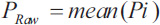 |
(5) |
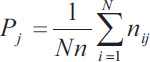 |
(6) |
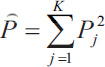 |
(7) |
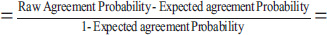 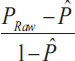
|
(8) |
Where n= number of raters; j= range of scores (j=1,..,k); i=number of patients (i=1,..,N).
Example 2: fourteen dentists give grades from 1 to 5 about the severity of a tooth's damage. If 5 patients are examined, the statistical value of Fleiss' kappa is calculated below (Table 4).
For our example in Table 3, P1 is 0.157. 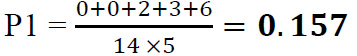
And taking the second row,
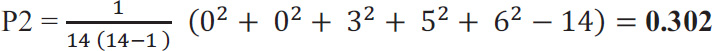
In order to calculate 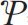 , we need to know the sum of Pi.
, we need to know the sum of Pi.
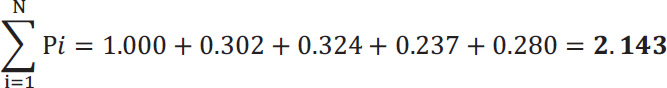
Over the whole sheet,
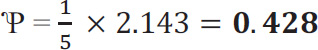
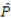 0.1572 + 0.1282 + 0.2712 + 0.1422 + 0.3002 = 0. 223
0.1572 + 0.1282 + 0.2712 + 0.1422 + 0.3002 = 0. 223
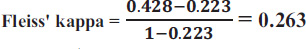 It shows a weak agreement.
It shows a weak agreement.
2.3. Cohen's Weighted Kappa
The weighted kappa penalizes disagreements in terms of their seriousness whereas the unweighted kappa treats all differences equally. Consequently, Cohen's weighted kappa ought to be employed when data is in the form of a graded ordinal scale. In this situation, three matrices such as observed score matrix, the expected score matrix based on agreement, and the weight matrix are involved. Weight matrix cells located on the diagonal indicate agreement and off-diagonal cells indicate disagreement. The equation for weighted kappa is: (Eq 9).
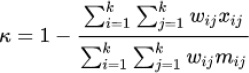 |
(9) |
where k = number of codes and Wij, Xij and Mij are elements in the weight, observed, and expected matrices, respectively. When diagonal cells contain weights of 0 and all off-diagonal cells weights of 1, this formula produces the same value of kappa as the calculation given above (Figs. 1 and 2).
| - | Categorical Scoring | - | ||||
|---|---|---|---|---|---|---|
| - | 1 | 2 | 3 | 4 | 5 | Pi |
| Patient 1 | 0 | 0 | 0 | 0 | 14 | 1.000 |
| Patient 2 | 0 | 0 | 3 | 5 | 6 | 0.302 |
| Patient 3 | 2 | 2 | 8 | 1 | 1 | 0.324 |
| Patient 4 | 3 | 2 | 6 | 3 | 0 | 0.237 |
| Patient 5 | 6 | 5 | 2 | 1 | 0 | 0.280 |
| Total | 11 | 9 | 19 | 10 | 21 | - |
| Kappa Value | Interpretation |
|---|---|
| < 0 | NO agreement |
| 0.01 – 0.20 | Slight agreement |
| 0.21 – 0.40 | Fair agreement |
| 0.41 – 0.60 | Moderate agreement |
| 0.61 – 0.80 | Substantial agreement |
| 0.81 – 1.00 | Almost perfect agreement |
| Types of Kappa | Calculation Formulas | Usage |
|---|---|---|
| Cohen's kappa |  |
Determine the level of agreement among two independent raters - ratings are based solely on nominal scales-lacks the ability to measure inter-rater reliability with more than two independent raters. In such cases, a suitable alternative is to utilize Krippendorff's alpha. |
| Fleiss' kappa | 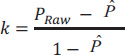 |
Determine the level of agreement among multiple independent raters, it can be used with binary or nominal-scale or ordinal or ranked data- it does not consider or account for the inherent order or hierarchy of categories within an ordinal variable.-it requires the random selection of patients and raters. |
| Cohen's weighted kappa | 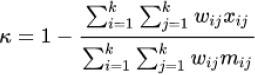 |
Determine the level of agreement among two independent raters - ratings are based on ordinal scales |
Landis and Koch (1977) gave the following table for interpreting Kappa values [18-20] (Table 5).
In short, the types of Kappa calculation methods are pre-sented in (Table 6). Using this table, researchers will be able to choose the type of kappa suitable for their research (Table 6).
Statistical software guideline:
SPSS:
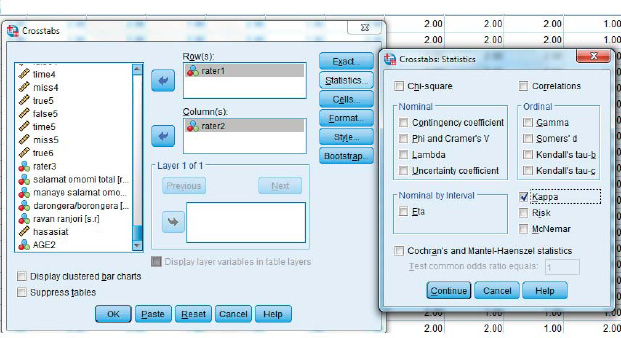
Cohen's kappa: Analysis  Descriptive statistics
Descriptive statistics  Cross tabs
Cross tabs
Cohen's weighted kappa:
The way to perform weighted kappa is the same as Cohen's kappa, only before going to the above analysis, weighting should be done in the following way:
Data  weight cases
weight cases
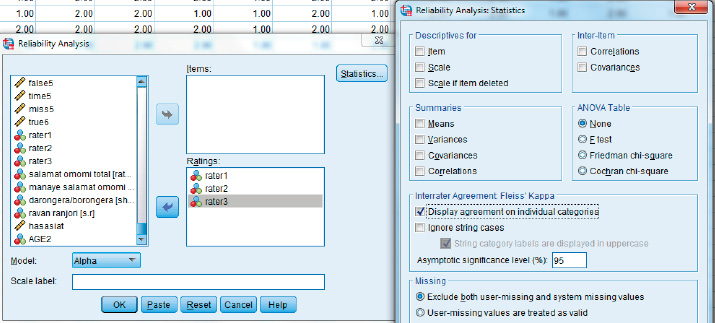
Fleiss' kappa: Analyze  scales
scales  reliability analysis
reliability analysis
R:
• Cohen's / Cohen's weighted kappa: the function 'kappa2' from the package 'irr',
• Other functions:
Cohen's unweight kappa: kappa Cohen (data, weight="unweighted")
Cohen's weighted kappa: kappa Cohen (data, weight="weighted")
Fleiss' kappa: function 'kappa m. fleiss' from the package 'irr
SATA:
Cohen's unweight kappa: kap rater1 rater2, tab
Cohen's weighted kappa: kap rater1 rater2 [fweight=wvar], tab
Fleiss' kappa: kap rater1 rater2 rater3
CONCLUSION
Cohen's kappa coefficient (κ) is a statistical measure utilized to assess the reliability between raters for qualitative items, both in terms of inter-rater and intra-rater reliability. In cross-classification, Cohen's weighted kappa is commonly employed as an agreement measure among raters(dentists). It serves as a suitable indicator for agreement when ratings are based solely on nominal scales without any inherent order structure. The original method of calculating Cohen's kappa lacks the ability to measure inter-rater reliability with more than two raters. In such cases, a suitable alternative is to utilize Krippendorff's alpha.
On the other hand, Cohen's weighted kappa is preferable when dealing with categorical data that possess an ordinal structure, such as rating systems with categories like high, medium, or low presence of a specific attribute. This weighted kappa places more emphasis on the seriousness of disagreements, while the unweighted kappa treats all disagreements as equally important. Therefore, the unweighted kappa is not suitable for ordinal scales.
Fleiss' kappa (κ), is another measure of inter-rater agreement, specifically employed to determine the level of agreement among multiple raters, it can be used with binary or nominal-scale data and can also be applied to ordinal or ranked data. However, in cases involving ordinal ratings, such as defect severity ratings on a scale of 1–5, Kendall's coefficients, which account for the ordering of categories, are usually more appropriate for determining association than kappa alone. Fleiss' kappa does not consider or account for the inherent order or hierarchy of categories within an ordinal variable.
CONSENT FOR PUBLICATION
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.

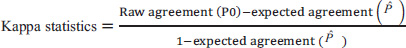
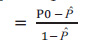 [
[
