All published articles of this journal are available on ScienceDirect.
VGG-16 based Deep Learning Approach for Cephalometric Landmark Detection
Abstract
Aims
The aim of this research work is to compare the accuracy and precision of manual landmark identification versus automated methods using deep learning neural networks.
Background
Cephalometric landmark detection is a critical task in orthodontics and maxillofacial surgery and accurate identification of landmarks is essential for treatment planning and precise diagnosis outcomes. It entails locating particular anatomical landmarks on lateral cephalometric radiographs of the skull that can be utilised to evaluate the relationships between the skeleton and the teeth as well as the soft tissue profiles. Many software tools and landmark identification approaches have been implemented over time to increase the precision and dependability of cephalometric analysis.
Objective
The primary objective of this research is to evaluate the effectiveness of an automated deep learning-based VGG-16 algorithm for cephalometric landmark detection and to compare its performance against traditional manual identification methods in terms of accuracy and precision.
Methods
The study employs a VGG16 transfer learning model on a dataset of skull X-ray images from the IEEE 2015 ISBI Challenge to automatically identify 19 cephalometric landmarks on lateral cephalometric radiographs. The model is fine-tuned to predict the precise XY coordinates of these landmarks enhancing the accuracy of cephalometric analysis by minimizing manual intervention and improving detection consistency.
Results
The experimental findings indicate that the presented cephalometric landmark detection system has attained Successful Detection Rates (SDR) of 26.84%, 41.57%, 59.89% and 94.42% in the 2, 2.5, 3 and 4mm precision range respectively and a Mean Radial Error (MRE) of 2.67mm.
Conclusion
This paper has presented an approach for cephalometric landmark detection using the VGG-16 model a widely used deep learning architecture in computer vision. Through the experiments it is shown that the VGG-16 model can achieve state-of-the-art performance on the task of cephalometric landmark detection. The results have demonstrated that the VGG-16 model can automatically extract relevant features from cephalometric images allowing it to accurately detect anatomical landmarks. It is also shown that fine-tuning the pre-trained VGG-16 model on cephalometric data can improve its performance on this task. The suggested technique may enhance the effectiveness and precision of cephalometric landmark detection and facilitate clinical decision-making in orthodontics and maxillofacial surgery.
1. INTRODUCTION
Cephalometric landmark detection is an important tool used in dentistry and orthodontics for treatment planning and precise diagnosis outcomes. The process involves identifying specific anatomical landmarks on lateral cephalometric radiographs of the skull, which can be used to assess the connections between the skeletal structure, teeth, and soft tissue profiles. Many software tools and landmark identification approaches have been imple- mented over time to increase the precision and dependability of cephalometric analysis. The findings of this study will offer vital knowledge about the advantages and drawbacks of various landmark detection techniques and aid in determining the most dependable and effective tools for cephalometric analysis in clinical settings. This research has an opportunity to potentially result in enhanced diagnostic and treatment planning, as well as improved treatment results for patients undergoing orthodontic and dental procedures. The field of cephalometric landmark detection has seen significant advancements with deep learning architectures in recent years.
In clinical practice, orthodontists often manually trace landmarks, a method that is both time-consuming and prone to inconsistencies, leading to unreliable results. Concerns have been raised about the significant variability between different observers and even within the same observer due to differences in training and experience. Given that accurate landmark estimation is crucial for pathology identification and treatment, manual cepha- lometric analysis can lead to serious consequences if done poorly. Therefore, there is a strong need for fully automated and reliable computerized systems that can accurately detect cephalometric landmarks, perform necessary measurements, and assess anatomical abnor- malities efficiently.
This paper is organized as: Section II discusses the resulted work and Section III discusses the proposed methodology for cephalometric landmark analysis. The dataset description, experimental setup, hyperparameter tuning, evaluation metrics, result analysis and the comparison with the state-of-art methods are discussed in section IV. The conclusion of the research work is detailed in section V.
2. RELATED WORK
Several studies have shown the effectiveness of convolution based neural networks (CNN) in automating the landmark identification process from cephalograms. A deep learning framework by Nishimoto et al. [1] to create cephalometric personal computer-based landmark detection algorithm. Lee et al. [2] proposed a landmark-dependent multi-scale patch-based method for landmark identification. A deep learning-based technique for automatic landmark localisation in medical images was put out by Noothout et al. [3]. Zeng et al. [4] developed a cascaded convolutional network-based method for cephalometric landmark detection. Other notable studies in this area include those by Song et al. [5], Lee et al. [6], Kim et al. [7], Qian et al. [8], Oh et al. [9], Kochhar et al. [10], Seo et al. [11], Arik et al. [12], Lee et al. [13], Lindner and Cootes [14], Lachinov et al. [15], Grau et al. [16], Mosleh et al. [17], and Pouyan and Farshbaf [18] utilised various artificial intelligence techniques to efficiently identify landmarks.
Ciesielski et al. [19] proposed a technique for identifying landmarks in cephalometric X-rays by employing genetic programming. Saad et al. [20] described a method for automatic cephalometric analysis that uses dynamic appearance models and simulated annealing. Rakosi et al. [21] suggested that a landmark error of 2 mm is tolerable when identifying cephalometric landmarks. Forsyth et al. [22] claimed that a 1 mm precision is ideal for cephalometric landmark detection. A landmark detection technique for cephalometric radiographs utilising pulse linked neural networks was proposed by Innes et al. [23]. Vucinic et al. [24] developed an automatic landmarking system for cephalograms using active appearance models. Kang et al. [25] proposed an automatic 3D cephalometric annotation system using 3D convolutional neural networks. By extracting features from the skull's symmetry, Neelapu et al. [26] established an automatic localization approach for 3D cephalometric landmarks on CBCT images. Codari et al. [27] proposed a computer-aided cephalometric landmark annotation method based on a point distribution model that utilizes both shape and appearance information for accurate landmark localization on CBCT data. Wang et al. [28] presented a multiresolution decision tree regression voting method for the automatic analysis of lateral cephalograms, where a decision tree structure is used to classify landmarks at different levels of detail for accurate detection.
Hutton et al. [29] evaluated the efficacy of active shape models in automatically identifying cephalometric landmarks. The models were trained using manually annotated landmarks and then tested on a collection of unknown landmarks. Vandaele et al. [30] developed a tree-based approach for automatic cephalometric landmark detection. Support vector machines (SVMs) were used by Chakrabartty et al. [31] to offer a reliable cephalometric landmark recognition approach. The SVM classifier was trained on a set of manually annotated landmarks and evaluated on a set of unknown landmarks. Romaniuk et al. [32] proposed a statistical localization model for landmarks, which includes both linear and non-linear components. The models were tested using a series of unknown landmark processing approaches after being trained on a set of annotated landmarks. Lindner et al. [33] introduced a completely automated system that accurately identifies and analyses cephalometric features in lateral cephalograms. The system uses a combination of deep learning and image processing methods to detect these landmarks.
Juneja et al. [34] provided a comprehensive review of various cephalometric landmark detection techniques, including deep learning-based methods, traditional image processing techniques, and hybrid methods that combine both approaches. Neeraja et al. [35] conducted a thorough examination and comparison of various AI techniques used to automate the recognition of cephalometric landmarks from X-ray images. According to Shahidi et al. [36], manual annotation carried out by a human expert was less accurate than computerised automatic detection of cephalometric landmarks. The results showed that the automated method was highly accurate and reliable for landmark identification. To identify landmarks on cephalometric radiographs, Kafieh et al. [37] proposed a modified active shape model with sub-image matching. The effectiveness of cellular neural networks for recognising cephalometric landmarks was assessed by Leonardi et al. [38]. Hwang et al. [39] developed an automated cephalometric landmark identification system using deep learning techniques, which outperformed human experts in terms of accuracy. A Random Forest (RF) based likelihood model was presented by Mirzaalian et al. [40] to enhance the performance of pictorial structures in cephalometric landmark detection. An adversarial encoder-decoder network was suggested by Dai et al. [41] to detect landmarks from cephalograms. The CephXNet architecture presented by Neeraja et al. [42] employed a customised CNN framework that integrates a Squeeze-and-excitation (SE) attention block to automatically predict 19 landmark coordinates. Gangani et al. [44, 45] analysed chronic kidney disease and diabetics using explainable AI in machine learning based techniques.
3. METHODS
The Visual Geometry Group (VGG) at the University of Oxford created the deep convolutional neural network architecture known as the VGG transfer learning model (VGGNet), as shown in Fig. (1a). The architecture was first presented in the 2014 ILSVRC (ImageNet Large Scale Visual Recognition Challenge) and has subsequently gained popularity and influence for a range of computer vision challenges. A number of convolutional and pooling layers precede fully connected layers that result in good prediction accuracy in the VGG model. The pooling layers are of 2x2 filters, and the convolutional layers are made up of 3x3 filters with stride 1. As the network becomes more complicated, the number of filters in each layer increases, creating a highly expressive and complex feature representation. The pre-trained VGG16 is used as a feature extractor in the model to create a convolutional neural network (CNN) utilising transfer learning. The design has a dense layer that receives the output from VGG16 and a final output layer with a sigmoid activation function that outputs the anticipated bounding box coordinates. With a test size of 10%, the data are divided into training and testing sets. The final step is to make predictions on a set of test images and compute the Euclidean distance between the actual values provided by doctors and the predicted points. The summary of the trained VGG16 models is shown in Fig. (1b) with 17,936,548 trained parameters.
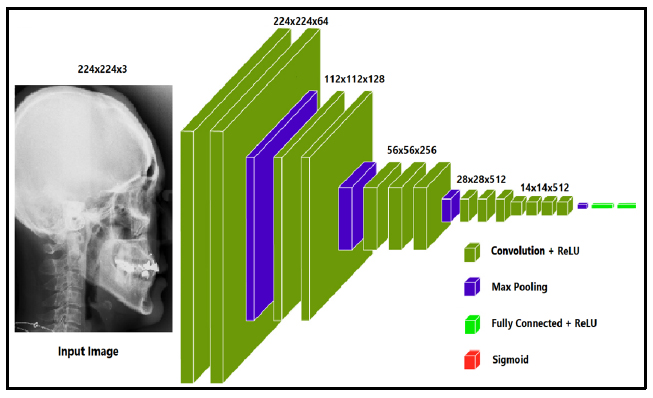
Proposed VGG-16 model architecture [43].
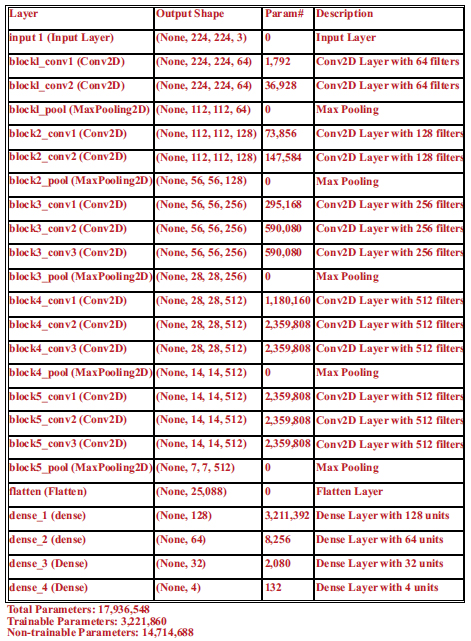
Summary of trained model for cephalometric landmark prediction.
The VGG-16 architecture, traditionally designed for image classification, has been adapted to predict bounding boxes for cephalometric landmark detection. Key modifications include flattening the output feature map after the final MaxPooling layer and passing it through a series of Dense layers, culminating in a final Dense layer with 4 units to output bounding box coordinates (x_min, y_min, x_max, y_max). This adaptation shifts the model's focus from class prediction to spatial localization, which is essential for precise cephalometric analysis in medical imaging.
4. RESULTS AND DISCUSSION
4.1. Dataset
The dataset used for the experiment is obtained from the 2015 ISBI IEEE challenge in automatically identifying the 19 landmarks. The dataset comprises 400 skull radiographs. The evaluation is conducted by utilising 360 images for training purposes and 40 images for testing purposes. The images were initially at a resolution of 1935×2400 pixels; however, the dimensions were later reduced to 224×224 pixels during the implementation process. The dataset included cephalometric X-ray images along with the 19 landmark coordinates and are shown in Fig. (2).
4.2. Experimental Setup
The proposed method was implemented with Anaconda (conda version: 23.1.0) as the installation system, Spyder 3.516 serving as the integrated development environment and Python 3.9 (python version: 3.9.13.final.0) was used as the programming language, TensorFlow was used to run the Python deep learning library Keras (version 2.11.0). OpenCV version 4.7.0, NumPy version 1.21.5, Matplotlib version 3.5.2, and Sklearn version 1.0.2 are the relevant libraries. The experiment uses an Intel(R) Core(TM) i7-8565U Processor running at 1.80 GHz and 1.99 GHz with 8 GB of memory is offered (7.79 GB usable). Adam optimizer was used for training the model.

Location of 19 landmarks provided by ISBI challenge [34].
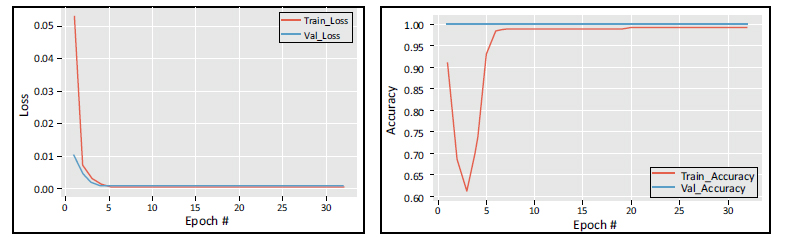
Training and validation loss and accuracy vs number of epochs.
4.3. Hyper-parameter Tuning
The system was finetuned by adjusting the three hyperparameters: batch size, learning rate, and number of epochs. The model underwent training for a total of 32 epochs, with each epoch included 10 iterations. The experiment utilised a batch size of 32 and a learning rate of 1e-4. The batch size, which specifies the number of samples analysed before updating the internal parameters of the model, was configured to 32. A batch size of 32 achieves a trade-off between efficient training and stable convergence, enabling the model to successfully learn from the data without overloading memory resources. The learning rate, an essential hyperparameter that controls the size of each step taken during iteration towards the minimum of the loss function, was assigned a value of 1e-4 (0.0001). Using a lower learning rate facilitates a better convergence of the model and prevents it from exceeding the optimal parameters. This is particularly important when finetuning a pre-trained model to reflect the specific attributes of cephalometric radiographs. The model completed 32 epochs of training, which involved processing the whole training dataset through the neural network in both forward and backward directions. The number of epochs was selected to strike a balance between allowing the model to learn from the data adequately and avoiding overfitting, which occurs when the model becomes overly specialised to the training data and performs poorly on unseen images. The training dataset was partitioned into smaller subsets (batches) that the model handled progressively. Each epoch consisted of 10 iterations. This strategy reduces the computational burden and allows for several changes to the model weights every epoch, hence improving the learning process.
4.4. Custom Model Training and Validation
Fig. (3) displays the mean squared error loss on the training set vs the number of epochs used for training. The ADAM optimizer was utilised to train the model for 30 epochs, with a learning rate of 0.01, enabling improved and faster convergence. The accuracy and loss curves are assessed for each fold of the training and validation sets. The training loss curve has a decreasing tendency as the number of training epochs grows, while a corresponding trend in the opposite direction is observed for the training accuracy. The suggested model helps maintain a consistent input distribution across different layers and reduces the likelihood of overfitting.
4.5. Evaluation Metrics
To calculate the number of pixels equivalent to 2 mm, we can divide 2mm2 by the area of one pixel, 2 mm2 / 0.573042 mm2 = 3.486. Therefore, 2 mm corresponds to approximately 3.486 pixels. Hence, 2mm = 3.486 pixels, 2.5mm = 4.35 pixels, 3mm = 5.229 pixels, 4mm = 6.972 pixels. To normalize the Euclidean distance since each image is resized, every Euclidean distance value obtained is divided by the normalization factor calculated (11.811). This factor is obtained as 300 pixels per inch translates to 11.811 pixels per mm. After dividing the distance by 11.811, if the final Euclidean distance lies within the pixel values determined above, it is accounted as successful detection of the landmark, and this adds up to the SDR. The MRE is calculated as the Euclidean distance between the detected landmark coordinates and the actual landmark coordinates. Therefore, the calculated Euclidean distances are combined and averaged to get the Mean Radial Error (MRE) for landmark ‘i’, as depicted in Eq. (1):
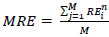 |
(1) |
where the number of images is ‘M’. The SDR was used for assessing the effectiveness of the landmark identification algorithms. It is the percentage of the landmarks that were successfully determined within 2, 2.5, 3, and 4mm detection ranges as given in Eqs. (2 and 3).
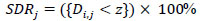 |
(2) |
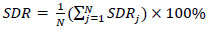 |
(3) |
where Di,j denotes the Euclidean distance between the jth predicted values of landmarks and ith image's ground truth values. Euclidean distance between two points in 2-D is defined as shown in Eq. (4). Mean Squared Error is defined in Eq. (5).
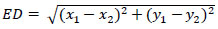 |
(4) |
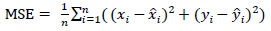 |
(5) |
4.6. Landmark Prediction Result Analysis
The proposed framework achieved an average SDR rate of 26.84%, 41.57%, 59.89% and 94.42% in 2mm,2.5mm,3mm and 4mm precision ranges. The average Mean Radial Error (MRE) for 19 landmarks is 2.67mm. The prediction results obtained for the 19 landmarks using VGG-16 architecture are shown in Table 1. The bounding box generated for the cephalometric landmarks is shown in Fig. (4). The landmark-wise Successful Detection Rate (SDR%) for all 19 landmarks in the 2, 2.5, 3, and 4mm ranges are plotted in Fig. (5).
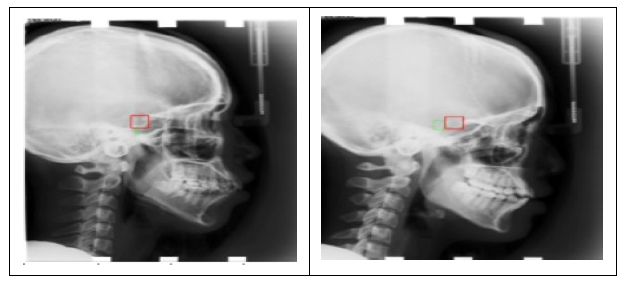
Bounding box generated are represented with the green box.
| Landmark |
MRE (in mm) |
Successful Detection Rate (mm) | |||
|---|---|---|---|---|---|
| 2mm | 2.5mm | 3mm | 4mm | ||
| 1 | 3.069 | 18 | 32 | 54 | 90 |
| 2 | 2.695 | 26 | 42 | 62 | 92 |
| 3 | 2.697 | 30 | 48 | 58 | 94 |
| 4 | 2.694 | 28 | 38 | 58 | 98 |
| 5 | 2.715 | 34 | 40 | 58 | 94 |
| 6 | 2.447 | 36 | 52 | 68 | 92 |
| 7 | 2.558 | 26 | 44 | 60 | 96 |
| 8 | 2.523 | 36 | 44 | 62 | 94 |
| 9 | 2.752 | 30 | 42 | 56 | 88 |
| 10 | 2.51 | 30 | 46 | 66 | 96 |
| 11 | 2.849 | 22 | 36 | 58 | 90 |
| 12 | 2.808 | 18 | 32 | 54 | 96 |
| 13 | 2.711 | 20 | 44 | 60 | 94 |
| 14 | 2.784 | 22 | 36 | 56 | 92 |
| 15 | 2.47 | 36 | 52 | 68 | 96 |
| 16 | 2.848 | 20 | 32 | 60 | 94 |
| 17 | 2.501 | 28 | 40 | 60 | 100 |
| 18 | 2.51 | 22 | 44 | 62 | 98 |
| 19 | 2.587 | 28 | 46 | 58 | 100 |
| Average | 2.67 | 26.84 | 41.57 | 59.89 | 94.42 |
| Best | 2.447 | 36 | 52 | 68 | 100 |
| Worst | 3.069 | 18 | 32 | 54 | 88 |
| Median | 2.695 | 28 | 42 | 60 | 94 |
4.7. Comparison with State-of-the-art Methods
Tables 2 and 3 compare the Successful Detection Rate (SDR%) within 2mm, 2.5mm, 3mm and 4mm and Mean Radial Error (MRE in mm) of various proposed methodologies. A Successful Detection Rate of 84.7% is obtained in 2mm precision range RFRV by Lindner et al. [33]. Noothout et al. [3] used a full CNN and achieved 80% SDR in 2mm precision range. Song et al. [5] used a deep convolution neural network to achieve 74% of SDR in 2mm precision range. To improve the Successful Detection Rate, Qian et al. [8] suggested Multi-head attention neural network (CephaNN) attaining 76.32% in 2mm precision. An Extremely Randomized Forests algorithm was proposed by Vandaele et al. [30] for automatically predicting the landmark coordinates and obtained an SDR of 77.58% for 2mm precision. A pictorial structure-based algorithm was investigated by Mirzaalian et al. [39], achieving 62.32% SDR for 2mm. A pattern-based detection algorithm on mathematical morphology techniques was introduced by Grau et al. [16] and obtained Mean Radial Error of 1.1mm. The Mean Radial Error (MRE) is reduced to 0.9mm using YOLOv3 by Hwang et al. [38]. Mosleh et al. [17] suggested an image processing approach to automatically analyse cephalometric landmarks and achieved an MRE of 0.16mm. Fig. (6) illustrates the comparison of SDR and MRE of the proposed model with various existing methodologies [46].
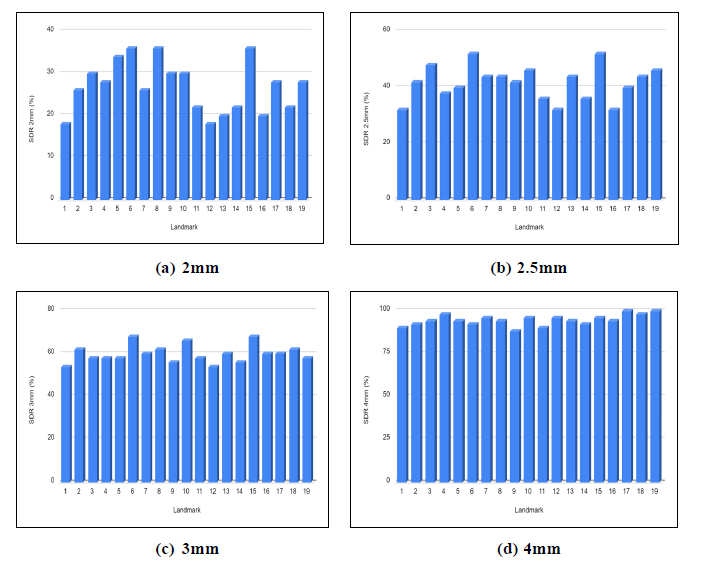
Landmark-wise SDR% for all 19 landmarks in the 2, 2.5, 3, 4mm precision ranges.
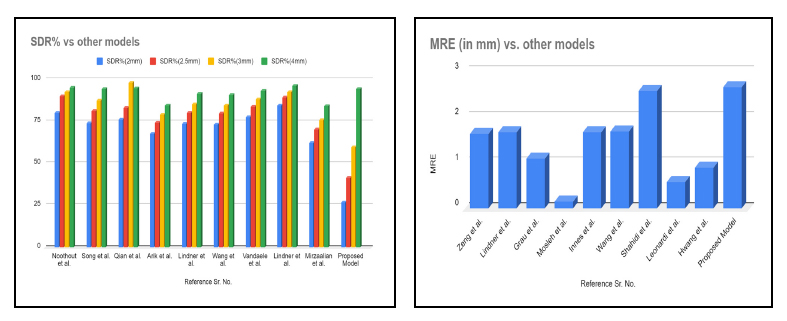
SDR% and MRE of the proposed model vs other models.
| Author/Refs | Methodology | Successful Detection Rate (SDR%) | |||
|---|---|---|---|---|---|
| 2mm | 2.5mm | 3mm | 4mm | ||
| Noothout et al. [3] | Fully Convolutional Neural Network (FCNN) | 80 | 90 | 92.5 | 95 |
| Song et al. [5] | Convolutional Neural Network (CNN) | 74 | 81.3 | 87.5 | 94.3 |
| Qian et al. [8] | Multi-head attention neural network (CephaNN) | 76.32 | 82.95 | 97.95 | 94.63 |
| Arik et al. [12] | Convolutional Neural Network (CNN) | 67.68 | 74.16 | 79.11 | 84.63 |
| Lindner et al. [14] | Random Forest based Regression-Voting in the Constrained Local Model framework (RFRV-CLM) | 73.68 | 80.21 | 85.19 | 91.47 |
| Wang et al. [28] | Multiresolution Decision Tree Regression Voting (MDTRV) algorithm | 73.37 | 79.65 | 84.46 | 90.67 |
| Vandaele et al. [30] | Extremely Randomized Forests | 77.58 | 83.89 | 88.37 | 93.21 |
| Lindner et al. [33] | Random Forest regression-voting (RFRV) | 84.7 | 89.38 | 92.62 | 96.3 |
| Mirzaalian et al. [40] | Pictorial structure-based algorithm | 62.32 | 70.42 | 75.68 | 84.05 |
| Author/Refs | Methodology | MRE (in mm) |
|---|---|---|
| Zeng et al. [4] | Convolutional Neural Network (CNN) | 1.64 |
| Lindner et al. [14] | Random Forest based Regression-Voting in the Constrained Local Model framework (RFRV-CLM) | 1.67 |
| Grau et al. [16] | Pattern detection algorithm based on mathematical morphology techniques | 1.1 |
| Mosleh et al. [17] | Image processing system | 0.16 |
| Innes et al. [23] | Pulse Coupled Neural Network (PCNN) | 1.68 |
| Wang et al. [28] | Multiresolution Decision Tree Regression Voting (MDTRV) | 1.69 |
| Shahidi et al. [36] | Knowledge-based approach | 2.59 |
| Leonardi et al. [38] | Cellular Neural Network | 0.59 |
| Hwang et al. [39] | YOLOv3 | 0.9 |
CONCLUSION
This paper has presented an approach to cephalometric landmark detection using the VGG-16 model, a widely used deep learning architecture in computer vision. The customised VGG-16 model achieved satisfactory performance in cephalometric landmark detection compared to state-of-the-art methods. The results have demonstrated that the VGG-16 model can automatically extract relevant features from cephalometric images, allowing it to accurately detect anatomical landmarks. It has also been shown that fine-tuning the pre-trained VGG-16 model on cephalometric data can improve its performance in this task. The experimental results demonstrate that the cephalometric landmark detection system achieved a Successful Detection Rate (SDR%) of 26.84%, 41.57%, 59.89%, and 94.42% within the precision ranges of 2mm, 2.5mm, 3mm, and 4mm, respectively. Additionally, the system exhibited a Mean Radial Error (MRE) of 2.67mm. The proposed technique has the potential to improve the accuracy and efficiency of identifying cephalometric landmarks, as well as aid in making clinical decisions in the fields of orthodontics and maxillofacial surgery.
AUTHORS’ CONTRIBUTION
It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.
LIST OF ABBREVIATIONS
| VGG | = Visual Geometry Group |
| SDR | = Successful Detection Rate |
| MSE | = Mean Squared Error |
| MRE | = Mean Radial Error |
| CNN | = Convolutional Neural Networks |
| CBCT | = Cone-beam computed tomography |
| PPI | = Pixels per inch |


