All published articles of this journal are available on ScienceDirect.
A New-fangled Classification Algorithm for Medical Heart Diseases Analysis using Wavelet Transforms
Abstract
Background
In this article, the Mixed Mode Database Miner (MMDBM) algorithm is introduced for the classification of data. This algorithm depends on the decision tree classifier, which handles the numerical and categorical attributes. For the experimental analysis in a well-explored heart disease data set collected from the UCI Repository.
Aims
Understanding the fundamentals of every classification method and how to apply them to CUDA is the aim of this study. After reviewing the literature, the approach that is most suited is selected for implementing the suggested algorithm in the MMDM classifier along with the discrete wavelet decomposition. From this experimental analysis, we observed that the use of the wavelet technique in the MMDBM algorithm provides better and more accurate results for data classification.
Objective
The main objective of the manuscript is to identify the early stage of heart attack that was caused either by smoking, smoking with tobacco, or non-smoking. Additionally, this study aims to check the validity of the MMDM classifier along with the discrete wavelet decomposition. From this experimental analysis, we observed that the use of the wavelet technique in the MMDBM algorithm provides better and more accurate results for data classification.
Methods
In the modern digital world today, data has a major impact on everyone’s life. Every database contains a lot of information hidden either in the form of numerical data, characteristic data, or a mixture of both. Moreover, to accurately decode every dataset, a fast and efficient classifier is essential.. Moreover, by using this hybrid technique based on both MMDBM and Wavelet processes, it compresses the data with minimum storage capacity.
Results
The experimental results are compared with the classified data to wavelet data output. These results prove that our presented technique is more prominent and robust in an analysis of heart diseases.
Conclusion
This algorithm is based on a decision tree classifier and tested on a heart disease database. MMDBM is applied to classify a large data set of numerical and categorical attributes. The data are compressed with the help of a one-dimensional wavelet transform. This is one of the new approaches applied to classified data in real-time applications.
1. INTRODUCTION
Data mining is a process of searching for the correct information from a large amount of data set. There are many techniques available in the research, such as Artificial Neural Networks [1], Genetic algorithms [2], Association rules, and Clustering [3]. Classification of the data has been considered one of the important techniques in data mining [4, 5]. Several different approaches are made to construct accurate classifiers, e.g., Bayesian classifier [6, 7], Decision tree [8, 9, 10], Support Vector Machine (SVMs) [11, 12, 13, 14] and associative classifiers [15]. In the classification of data, the training data set is given as input data. The input data consists of two attributes: numerical attribute and categorical attribute or alpha-numeric attribute. For example, Cp represents the Chest Pain type of a patient, Fbs represents the Fasting blood sugar of a person that falls under the category of a numerical attribute, Furthermore, the categorical attribute has values from an unordered domain, such as whether the person is illiterate or literate, male or female, and so on [3, 16, 17]. Classification is the method of splitting a dataset into another group, called a class, which depends on suitable attributes. A rule-based algorithm can generate multiple splitting points of the concept [18, 19, 20]. In this algorithm, a set of rules is framed as follows:
IF < conditions > THEN < (class value) >
The algorithm is applied to each node, and if the “IF” condition is satisfied, it travels to the left side of the node, or if the “IF” condition is not satisfied, it travels to the right side of the node, or “else” the condition is counting the missing values. This rule is applied to all the attributes. Finally, it counts the class value.
A Wavelet transform is a mathematical transform that was applied in various branches of science and engineering, such as geology, signal processing, astronomy, and computer science. The wavelet transform's ability to divide the data, or functions, into discrete data elements accounts for its success. Subsequently, it examines every element independently using a matching resolution [21].
Thus, it provides more information about the data in an informative manner [22]. In recent years, many computer software packages have been easily available to perform wavelet transforms in an elegant approach. The availability of more wavelet packages has gained the most popularity among engineers.
In this paper, the Haar wavelet algorithm is applied to the MMDBM algorithm result (Refer to Tables 1-2). This proposed (MMDBM) method is the best classifier compared to 19 supervised learning techniques (Including SVM and KNN) and has a higher rate of accuracy in detecting breast cancer cases from the given datasets [13]. In a study [23], eight supervised learning methods using eight different types of databases are compared. The proposed method, the MMDBM algorithm, is accomplished with the highest accuracy rate. The proposed algorithm is more prominent and robust considering all aspects of accuracy and computational time.
The structure of this document is as follows. In Section 2, the relevant works addressed are discussed. In Section 3, MMDBM algorithms are briefly covered. In Section 4, the results of an experimental evaluation based on the MMDBM algorithm are explained, and the histogram of each distribution is computed. The conclusion is discussed in Section 5.
2. RELATED WORKS
The MMDBM algorithm depends on two algorithms, namely SLIQ and SPRINT. SLIQ means Supervised Learning in Quest. This algorithm was created by the IBM group under the direction of Rakesh Agrawal in the 1990s to determine processing time using both numerical and categorical variables. In addition, to determine the tree growth phase, he developed a method known as pre-sorting [17]. SPRINT is another classifier, which is a parallel algorithm developed by the same group at the end of the '90s. It is a planned classification that shows the decision-tree method's memory constraints are removed and demonstrates how quick and effective the intended algorithm is as a classifier [17, 23-25].
A new decision tree classifier known as the MMDBM algorithm handles both numerical and categorical attributes in huge datasets. This classifier can manage huge databases with a broad set of data or a huge number of binary attributes. Here, all the numerical attributes and qualifying midpoints are taken into consideration. However, this point is calculated at every level of the Gini index. Every distribution of the considered position is taken for examination in histogram estimation.
The first step is sorting the entire attribute and then taking the midpoint. This midpoint is not static due to inserting one record in this dataset. The midpoint is automatically changed. This proposed algorithm dynamically changes the midpoint value of each execution of the program.
The following is the basic concept of the Gini-Index theory. It can be assumed that S is a collection of s samples with k distinct classes (Ci,i = 1,...,k). Among the samples (Si, i = 1,...,k), there are the k subsets of S, which are partitioned based on the differences in classes. It can also be assumed that Si is the sample set from class Ci. Thus, set S's Gini-Index is:
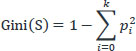 |
Where Pi is the probability that any sample belongs to Ci, it is calculated using si/s. Since all of the set's members fall into the same class and Gini(S) has a minimum of 0, the greatest amount of meaningful information may be gleaned. The least amount of meaningful information may be gathered when Gini(S) is at its maximum, which happens when all of the samples in the set are distributed evenly for each class. Nevertheless, the majority of Gini-Index research has simply divided decision tree features.
This paper used 30000 records in the Heart disease dataset taken from the UCI repository. In the final phase, 9365 records are counted for patients who smoke regularly, 7134 records for those who do not smoke, 6679 documents for those who smoke tobacco, and 6822 records for missing data.
The Gini index for the overall collection of the above original dataset is:
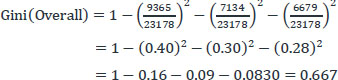 |
The Gini index for the overall class is updated. Similarly, the gini index for other attributes like Sex, Age, CP, Fbs, Trestps, and Year are found using the above gini equation.
There are two sections to this algorithm. The algorithm is explained in depth in the first section using a predictive classifier, and the Java program implementation is provided in the second section on object-oriented design [1, 3]. Furthermore, to check the validity of our classifier (MMDBM), we must have a large data set from which we obtain the medical data (no specific reason for choosing the heart database) from the UCI repository.
In a study [23, 26], the time and space complexity of the MMDBM Algorithm with efficient parallel quick sort and radix sort algorithms in GPU are discussed, which results from the Comparison of computational acceleration ratio (speed-up) and efficiency of processing time of CPU and GPU computing in MMDBM Classifier. The main results are used to compare the classifier with an existing CPU- quick sort and radix sort for the MMDBM classifier and GPU- quick sort and radix sort algorithms provide rapid and exact results with minimum execution time and support real-time applications.
2.1. MMDBM Algorithm
In this section, we briefly outline the algorithm procedure to classify the node values for any database. Let us consider a database consisting of ‘n’ attributes, and it is denoted as {a1, a2... an}, which acts as the Input of our algorithm. The output of the algorithm is node count as well as the construction of the decision tree. Let us explain the algorithm using a step-by-step procedure.
1. Extract all the attribute values from the database
2. Change sex from a categorical attribute to a numerical value attribute. Assign the numerical value for the male as zero and the female as 1. However, in our data, we have two generics to analyze the date we are assigning the numbers 0 for female and 1 for male for checking the IF conditions.
3. Arrange the input values using the quick sort algorithm. For taking the midpoint value of all attributes such as Sex, Age, Cp, Fbs, Trestbps, and Year. We are sorting all the data.
4. Obtain the midpoint value of every attribute.
5. The attribute name is denoted as ai, represents an attribute, vi represents the middle value of an attribute, and assigns the value as C as zero in the class value and M value as zero in the missing value. Iterate the above procedure
For I = 1 To N // where “N” denotes all the attribute nodes
Examine the attribute of all cases from the database
IF ai ≤ vi Condition satisfied it goes to the left end of the child node and scans all the nodes.
IF (a1 ≤ v1) AND (a2 ≤ v2) AND........ AND (an ≤ vn) THEN C
The above condition satisfies the count of the class value of each step
If the same value exists after performing the above operations, then update the appropriate class count value by assigning
C= C + 1
Otherwise
IF ai ≤ vi is not satisfied, it automatically goes to the right end of the node and then scans all the nodes. Now, once again count the class value, if the same value exists, then update the class value as follows.
C= C + 1
Otherwise
Count the missing value and then update as follows.
M= M + 1
and stop the iteration.
Get all result node values list class values from the database and place it in the appropriate count value.
| N1 | sex=M Node goto N2 else N3 | N23 | Trestbps<=4 Node goto N46 else N47 | N45 | Year<=4 Node goto N90 else N91 |
| N2 | Age<=35 Node goto N4 else N5 | N24 | Trestbps<=4 Node goto N48 else N49 | N46 | Year<=4 Node goto N92 else N93 |
| N3 | Age<=35 Node goto N6 else N7 | N25 | Trestbps<=4 Node goto N50 else N51 | N47 | Year<=4 Node goto N94 else N95 |
| N4 | CP<=48 Node goto N8 else N9 | N26 | Trestbps<=4 Node goto N52 else N53 | N48 | Year<=4 Node goto N96 else N97 |
| N5 | CP<=48 Node goto N10 else N11 | N27 | Trestbps<=4 Node goto N54 else N55 | N49 | Year<=4 Node goto N98 else N99 |
| N6 | CP<=48 Node goto N12 else N13 | N28 | Trestbps<=4 Node goto N56 else N57 | N50 | Year<=4 Node goto N100 else N101 |
| N7 | CP<=48 Node goto N14 else N15 | N29 | Trestbps<=4 Node goto N58 else N59 | N51 | Year<=4 Node goto N102 else N103 |
| N8 | Fbs<=4 Node goto N16 else N17 | N30 | Trestbps<=4 Node goto N60 else N61 | N52 | Year<=4 Node goto N104 else N105 |
| N9 | Fbs<=4 Node goto N18 else N19 | N31 | Trestbps<=4 Node goto N62 else N63 | N53 | Year<=4 Node goto N106 else N107 |
| N10 | Fbs<=4 Node goto N20 else N21 | N32 | Year<=4 Node goto N64 else N65 | N54 | Year<=4 Node goto N108 else N109 |
| N11 | Sport<=4 Node goto N22 else N23 | N33 | Year<=4 Node goto N66 else N67 | N55 | Year<=4 Node goto N110 else N111 |
| N12 | Fbs<=4 Node goto N24 else N25 | N34 | Year<=4 Node goto N68 else N69 | N56 | Year<=4 Node goto N112 else N113 |
| N13 | Fbs<=4 Node goto N26 else N27 | N35 | Year<=4 Node goto N70 else N71 | N57 | Year<=4 Node goto N114 else N115 |
| N14 | Fbs<=4 Node goto N28else N29 | N36 | Year<=4 Node goto N72 else N73 | N58 | Year<=4 Node goto N116 else N117 |
| N15 | Fbs<=4 Node goto N30 else N31 | N37 | Year<=4 Node goto N74else N75 | N59 | Year<=4 Node goto N118 else N119 |
| N16 | Trestbps<=4 Node goto N32 else N33 | N38 | Year<=4 Node goto N76 else N77 | N60 | Year<=4 Node goto N120 else N121 |
| N17 | Trestbps<=4 Node goto N34 else N35 | N39 | Year<=4 Node goto N78 else N79 | N61 | Year<=4 Node goto N122 else N123 |
| N18 | Trestbps<=4 Node goto N36 else N37 | N40 | Year<=4 Node goto N80 else N81 | N62 | Year<=4 Node goto N124 else N125 |
| N19 | Trestbps<=4 Node goto N38 else N39 | N41 | Year<=4 Node goto N82 else N83 | N63 | Year<=4 Node goto N126 else N127 |
| N20 | Trestbps<=4 Node goto N40 else N41 | N42 | Year<=4 Node goto N84 else N85 | N64 | Terminated 100% with S |
| N21 | Trestbps<=4 Node goto N42 else N43 | N43 | Year<=4 Node goto N86 else N87 | N65 | Terminated 100% with NS |
| N22 | Trestbps<=4 Node goto N44 else N45 | N44 | Year<=4 Node goto N88 else N89 | N66 | Terminated 100% with ST |
2.2. Best- Split point Method
Every node has a split point applied to it by computing the matching middle values. It analyzes every feature of every record in the data sets. Utilizing the conditional relation, categorize the node as follows:
IF (a1 ≤ v1) AND (a2 ≤ v2) AND..... AND (an ≤ vn) THEN C (class value) rule [5, 17] as shown in Table 1.
A series of conditions are contained in the If Conditions, Then Class rule antecedent (IF portion), which is typically joined by the logical conjunction operator (AND) [2, 7, 17]. Fig. (1) will be used to refer to each rule that is conducted.
1. This rule goes to the left-end side of another node called age if (Sex == F (or) M) is satisfied; if not, it automatically moves to the right-end side of that node. The age node's midpoint value determines the next splitting point.
2. The next splitting point is based on the mid-point value of CP. If the rule is satisfied (Sex= =M (or) F and Age ≤ (or) > mid-point value), it goes to the left-end node; if it is not satisfied, it goes to the right end of another node called weight.
3. This rule is false; it travels to the right-end side of another node called FBS, and it is satisfied if (Sex == M (or) F AND Age ≤ (or) > mid-point value AND CP ≤ (or) > mid-point value). Based on the FBS midpoint value, the next splitting point is determined.
4. The next dividing point is based on the mid-point value of Trestbps. If the condition (Sex == M (or) F AND Age ≤ (or) > mid-point value AND CP ≤ (or) > mid-point value AND FBS ≤ (or) > mid-point value) occurs, the rule is true and it goes to the left-end node. If the condition is satisfied, it travels to the right end of another node.
5. The next splitting point is based on the mid-point value of Years if (Sex == M (or) F AND Age ≤ (or) > mid-point value AND CP ≤ (or) > mid-point value AND Fbs ≤ (or) > mid-point value AND Trestbps ≤ (or) > mid-point value) is true. This rule goes to the left end of the node. The rule is false. It goes to the right end of another node year.
6. The next splitting point is based on the mid-point value of Years if (Sex == M (or) F AND Age ≤ (or) > mid-point value AND CP ≤ (or) > mid-point value AND Fbs ≤ (or) > mid-point value AND Trestbps ≤ (or) > mid-point value) is true. This rule goes to the left end of the node. The rule is false. It goes to the right end of another node year.
7. Update the class value once all operations have been completed. The count value is updated if the same value is present; if not, the missing count is updated, and so on. Based on the anticipated principles, the node count distribution is assessed (Fig. 1). Utilizing a decision tree built from the database, the classification nodes' histogram is computed.
3. METHODOLOGY
Moreover, To test the robustness of our classification algorithm, we studied from the medical database where the risk person affected by Heart disease has the habit of smoking, non-smoking, and smoking with tobacco data obtained from the UCI repository. The distribution of the node count value is based on the predicted rules obtained from the database, as represented in Fig. (1). The data sets that hold entries for the characteristics mentioned above.
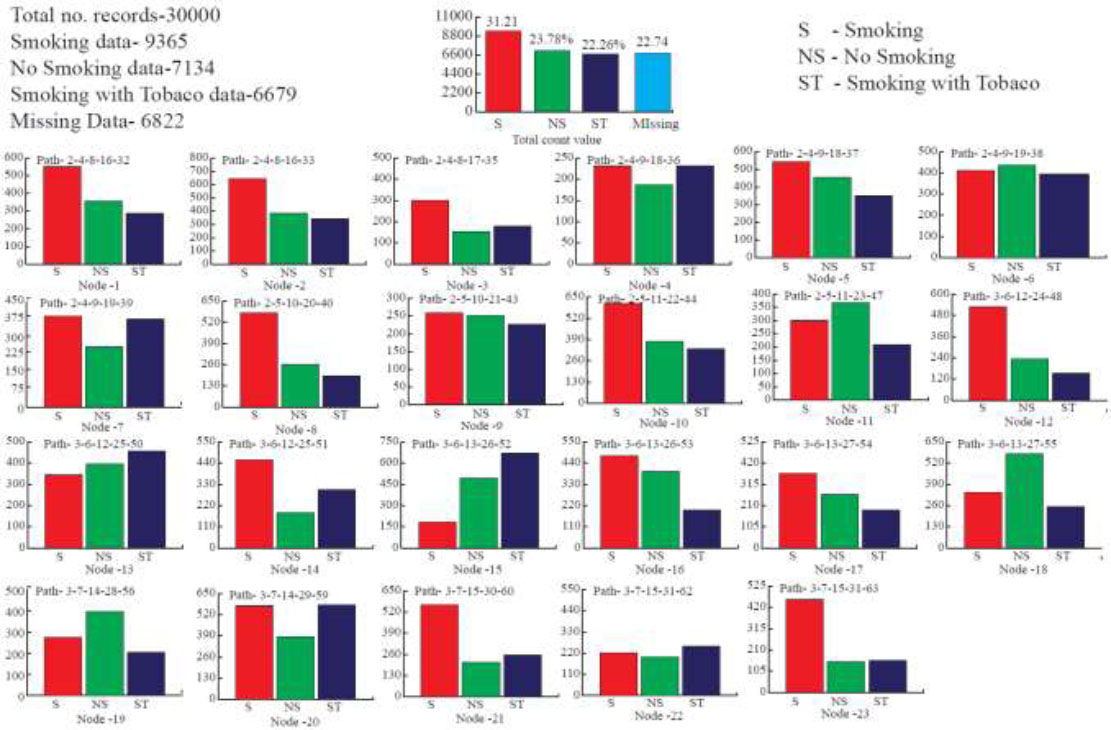
Distribution of the node count values.
This algorithm uses two categorical attributes, 'Sex' and 'Smoking.' The 'Sex' attribute is categorized as male or female, while 'Smoking' is categorized as S-Smoking, NS-No Smoking, and ST-Smoking with Tobacco. In addition to these, five numerical attributes are considered, such as 'Age' representing the person's age, and 'Cp,' which denotes the chest pain type.It assigns Value 1 for typical angina, Value 2- for typical angina, and Fbs denotes the Fasting blood sugar. If Fb >120 mg/dI, then Trestbps (resting blood pressure in mm Hg at hospital admission) and Year (total number of years smoked) are 1=true; 0 is false.
We have used 30000 records in the Heart disease dataset from the UCI repository. The proposed MMDBM algorithm checks the condition from the root node to the terminal node, which is called one distribution. If any one of the values is missing from this distribution, it is considered as one missing value, and again, the missing value is repeated in the same distribution. Then, the missing count value is updated as M=M+1. The code has already been created for those missing values in our data pre-processing, as mentioned in section 2.1. In our MMDM algorithm, there is no need to classify those missing values (in the cell), outliers, or feature selection.
Thus, under the above assumptions. We classified all the attributes where 23 different distributions of the nodes were noted and more than 30,000 records of patients with Heart disease problems were analyzed. Finally, it counts the number of patients with the habit of smoking data – 9365 records, No Smoking- 7134 records, Smoking with Tobacco- 6679 records, and missing data-6822 records. Each distribution has been produced by various IF < condition >, followed by the Then rule.
This rule is dynamically constructed based on the predicted rule of the class count values. The traveled path and node count distributions are determined, and they are shown in Fig. (2) and Table 1.
Additionally, to categorize all the attributes, a classification tree is ultimately built. As a result, we can obtain the traveling path and distribution of 23 node count values for each of the 30,000 examples (see Table 2).
Wavelet means a small function with finite compact support denoted by the symbol
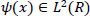 whose translations and dilation
whose translations and dilation
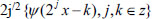 form an unconditional basis [27]. The wavelet can break down a piece of data into many smaller parts without changing the information contained in the original data since it forms an unconditional basis. Thus, each piece of data that contains complicated information can be represented in a simple form by using wavelet transform. In data mining processes, discrete wavelet transform (DWT), which is predicated on the Multiresolution Analysis (MRA) tool, is the key concept. The multiresolution analysis is Hilbert Space decomposition. L2(R) on a series of closed subspaces
form an unconditional basis [27]. The wavelet can break down a piece of data into many smaller parts without changing the information contained in the original data since it forms an unconditional basis. Thus, each piece of data that contains complicated information can be represented in a simple form by using wavelet transform. In data mining processes, discrete wavelet transform (DWT), which is predicated on the Multiresolution Analysis (MRA) tool, is the key concept. The multiresolution analysis is Hilbert Space decomposition. L2(R) on a series of closed subspaces
 such that it satisfies the following mathematical properties [28-30].
such that it satisfies the following mathematical properties [28-30].
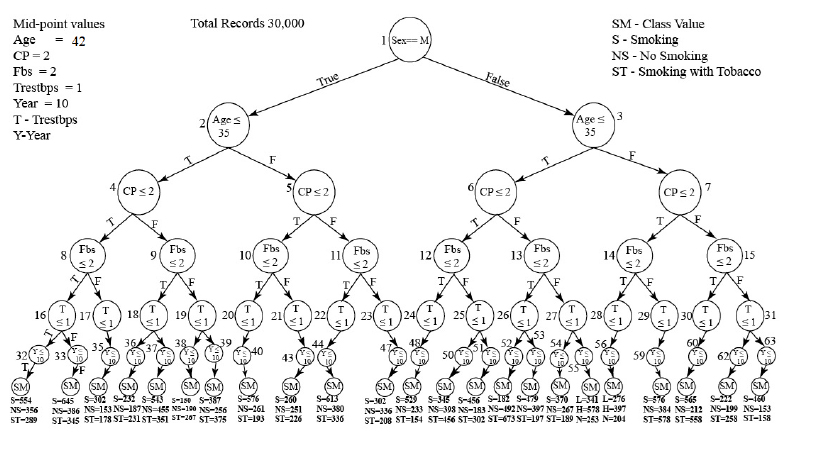
Classification tree in heart disease database.
| Classified Node Values | Class Count for Smoking, No Smoking, Smoking with Tobacco | ||||||
|---|---|---|---|---|---|---|---|
| Smoking | No Smoking | Smoking with Tabacco | |||||
| 2 | 4 | 8 | 16 | 32 | 554 | 356 | 289 |
| 2 | 4 | 8 | 16 | 33 | 645 | 386 | 345 |
| 2 | 4 | 8 | 17 | 35 | 302 | 153 | 178 |
| 2 | 4 | 9 | 18 | 36 | 232 | 187 | 231 |
| 2 | 4 | 9 | 18 | 37 | 543 | 455 | 351 |
| 2 | 4 | 9 | 19 | 38 | 150 | 190 | 267 |
| 2 | 4 | 9 | 19 | 39 | 387 | 256 | 375 |
| 2 | 5 | 10 | 20 | 40 | 576 | 261 | 193 |
| 2 | 5 | 10 | 21 | 43 | 260 | 251 | 226 |
| 2 | 5 | 11 | 22 | 44 | 613 | 380 | 336 |
| 2 | 5 | 11 | 23 | 47 | 302 | 366 | 208 |
| 3 | 6 | 12 | 24 | 48 | 529 | 233 | 154 |
| 3 | 6 | 12 | 25 | 50 | 345 | 398 | 456 |
| 3 | 6 | 12 | 25 | 51 | 456 | 183 | 302 |
| 3 | 6 | 13 | 26 | 52 | 182 | 492 | 673 |
| 3 | 6 | 13 | 26 | 53 | 479 | 397 | 197 |
| 3 | 6 | 13 | 27 | 54 | 370 | 267 | 189 |
| 3 | 6 | 13 | 27 | 55 | 341 | 578 | 253 |
| 3 | 7 | 14 | 28 | 56 | 276 | 397 | 204 |
| 3 | 7 | 14 | 29 | 59 | 576 | 384 | 578 |
| 3 | 7 | 15 | 30 | 60 | 565 | 212 | 258 |
| 3 | 7 | 15 | 31 | 62 | 222 | 199 | 258 |
| 3 | 7 | 15 | 31 | 63 | 460 | 153 | 158 |
i) Each Closed Subspace is contained in one another.
ii) The union of Closed Subspace is equal to the original space.
iii) The closed subspace forms a Reisz basis for L2(R).
The consequences of the MRA is that it decomposes the Hilbert space as,
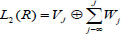 and another one,
and another one,
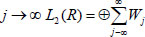 .
.
Thus, any data can be split as an orthogonal sum of the scaling function at the J level and as a wavelet function. The rapid discrete wavelet transform algorithm is the direct use of multiresolution analysis in data mining. The goal is to maintain detail while following an iterative process to make the data smooth. Which is to analyze projections of f to Wj.
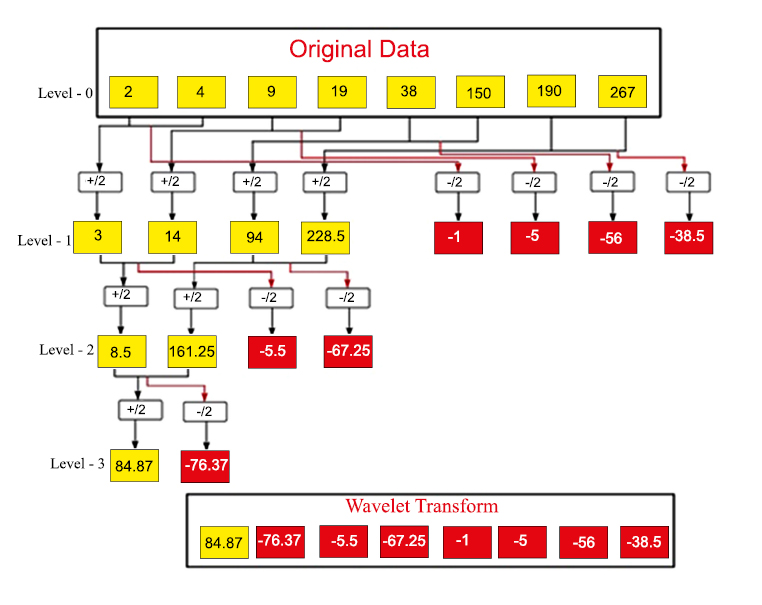
We use the Haar wavelet transforms algorithm to improve the data after it has been classified. The basic concept is to use the one-dimensional discrete Haar wavelet transform shown in Fig. (3) to classify the original data into different levels.
Process flow of wavelet transform.
4. RESULT AND DISCUSSIONS
Consider the discrete data obtained after applying the MMDBM algorithm. Represent the data as d1 = (d1, d2, d3…....dN ), where N is the positive even integer. Haar transform splits the discrete data into two sub-data of half its length. The first sub-data represents an average, which contains the approximate information of the input data, and another sub-data represents a difference average, which contains the detailed information of the input data.
The first average of sub-data, d1 = (d1, d1, ... , dN/2) , for the data d is calculated by taking the mean value. Its initial value, d1, is calculated by fetching the mean of the initial pair of values d: (d1 + d2)/2. Likewise, its next value d2 is calculated by fetching the mean of the next pair, which is d2 =(d3+d4)/2. Following this procedure, each value of d1 is generated by using a series of consecutive input data value pairs. The particular formula for d1 is dm = (d2m-1+d2m)/2 where m = 1,2,3,..N/2 correspondingly, another sub-data known as difference average denoted as e1 = (e1, e2, e3,....eN/2) is computed by taking the difference average. This is how it can be computed as a difference. Its initial value, e1 is determined by dividing the difference between the first two values of d by half. that is e1 = (d3-d4)/2.
Likewise e2 is computed by the second pair as e2 = (d3-d4)/2
| Approximation Information | Detailed Information |
|---|---|
| 3 = (2+4)/2 | -1 = (2-4)/2 |
| 14 = (9+19)/2 | -5 = (9-19)/2 |
| 94 = (38+150)/2 | -56 = (38-150)/2 |
| 228.5 = (190+267)/2 | -38.5 = (190-267)/2 |
Continuing in this process, all the values e1 are calculated, permitting the resulting general formula em = (d2m-1-d2m)/2 where m = 1,2,3……..N/2.
For example, consider the data obtained after applying the MMDBM algorithm in Table 2 as a = (2, 4, 9, 19, 38, 150, 190, 267). The Level-1 Haar wavelet transform is obtained by following the aforementioned approach as = (a1|d1), where d1 = (3 14 94 228.5) and e1 = (-1 -5 -56 -38.5), which is explained in the table below (Table 3).
After obtaining the Level-1 of Haar discrete wavelet transform, it is easy to obtain the Level-2 transform. Level-2 Haar wavelet transform can be obtained from Level-1 as follows. The second level average d2 and difference e2 is obtained from the approximation of the first Level d1. The approximation information is considered: d1 = [3 14 94 228.5] obtained from Level-1 as initial data for Level 2. Applying the same procedure described above, we obtained d2 = [8.5 161.25] and e2 = [-5.5 -67.25] (Table 4).
| Approximation Information | Detailed Information |
|---|---|
| 8.5= (3+14)/2 | -5.5 = (3-14)/2 |
| 161.25 = (94+228.5)/2 | -67.25 = (94-228.5)/2 |
Thus Level-2 Haar wavelet transform of input data f = (d2|e2|d1) = (8.5 161.25 | -5.5 -67.25| -1 -5 -56 -38.5). Similarly, Level-3 Haar wavelet transform can be obtained from Level-2 as follows. The third level average d3 and difference average e3 are obtained from the approximation of the second level d2.
Thus Level-3 Haar wavelet transform of input f = (d3|e3|d2|d1) = (84.87 |-76.37| -5.5 -67.25| -1 -5 -56 -38.5) (Table 5).
| Approximation Information | Detailed Information |
|---|---|
| 84.87 = (8.5+161.25)/2 | -76 .37= (8.5-161.25)/2 |
Thus the initial classified data (2 4 9 19 38 150 190 267) is changed into another data using wavelet transform as (84.5 -76.37 -5.5 -67.25 -1 -5 -56 -38.5). Thus, we applied wavelet transform for all the classified data in Table 2, and the output is shown in Table 6.
| O/P Wavelet Transform | |||||||
|---|---|---|---|---|---|---|---|
| 84.5 | -76.3 | -5.5 | -67.2 | -1 | -5 | -56 | -38.5 |
| 89.8 | -81.2 | -5.2 | -37.5 | -1 | -4.5 | -98 | -22 |
| 126.1 | -114.8 | -6.7 | 47.5 | -1.5 | -6 | -240.5 | 39.5 |
| 128.2 | -220.5 | -8 | -67.2 | -2 | -7 | -110 | 96.5 |
| 157.6 | -150.1 | -4.5 | -14.7 | -1 | -4 | -261 | 33.5 |
| 116.1 | -103.8 | -7.7 | -8 | -1.5 | -7 | -154 | 39 |
| 173 | -161 | -7.5 | -217 | -1.5 | -6.5 | -6.5 | -90.5 |
| 145.6 | -132.1 | -8.7 | 43.7 | -2 | -7.5 | -252.5 | -22 |
| 176.6 | -166.6 | -13 | -14.7 | -1.5 | -5.5 | -284.5 | 22 |
| 99.6 | -85.6 | -9 | -43.2 | -2 | -8 | -80 | -29.5 |
| 138.3 | -129.1 | -5.7 | 40.5 | -1.5 | -5 | -268 | 34 |
| 146.7 | -134.7 | -7.5 | -15.5 | -1.5 | -6.5 | -213 | 100 |
| 205.7 | -192.3 | -8.2 | -80.2 | -2 | -7.5 | -258.5 | -94.5 |
| 102.2 | -92.7 | -6 | -43.5 | -1.5 | -5.5 | -108.5 | 12.5 |
| 93.3 | -79.3 | -9 | 88.7 | -2 | -8 | -198.5 | -2.5 |
| 136.3 | -127.8 | -5.5 | -51.2 | -1 | -5 | -174 | -59.8 |
| 120.5 | -110.2 | -6.7 | -56.2 | -1.5 | -6 | -127.5 | 79 |
| 159.2 | -147.5 | -7.2 | -108.7 | -1.5 | -6 | -143 | 162.5 |
| 177.3 | -169.1 | -5.2 | -56.5 | -1 | -4.5 | -253 | 52 |
| 87.3 | -79.6 | -4.7 | 1.5 | -1 | -4.5 | -133.5 | -12.5 |
| 79.7 | -68.2 | -7 | -94.5 | -1.5 | -6.5 | -202.5 | -59.5 |
| 161.8 | -150.3 | -7 | -114.7 | -1.5 | -6.5 | -147.5 | -29 |
| 181.2 | -173.2 | -4 | -15.5 | -1 | -4 | -306 | 16 |
CONCLUSION
In this paper, the researchers presented a novel data categorization algorithm based on Mixed Mode Database Miner (MMDBM). This algorithm is based on a decision tree classifier and tested on a heart disease database. MMDBM is applied to classify a large amount of data sets with both numerical and categorical attributes. Thus, an array is used to hold classified data. The data are compressed with the help of a one-dimensional wavelet transform. Moreover, by utilizing one of the properties of wavelet, the data are represented differently without affecting the dimensionality of the data. The experimental results are compared with the classified data to wavelet data output. These results prove that our presented technique is more prominent and robust in the analysis of heart diseases. This is one of the new approaches applied to classified data in real-time applications.
AUTHORS’ CONTRIBUTION
It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.
LIST OF ABBREVIATIONS
| SVMs | = Support Vector Machine |
| MRA | = Multiresolution Analysis |
| DWT | = Discrete Wavelet Transform |


