All published articles of this journal are available on ScienceDirect.
Multiple Events Model for the Infant Mortality at Kigali University Teaching Hospital
Abstract
Introduction:
The present study applies multiple events survival analysis to infant mortality at the Kigali University Teaching Hospital (KUTH) in Rwanda.
Materials and Methods:
The primary dataset consists of newborns from KUTH recorded in the year 2016 and in the current paper, a complete case analysis was used. Two events per subject were modeled namely death and the occurrence of at least one of the following conditions that may also cause long-term death to infants such as severe oliguria, severe prematurity, very low birth weight, macrosomia, severe respiratory distress, gastroparesis, hemolytic, trisomy, asphyxia and laparoschisis. Covariates of interest include demographic covariates namely the age and the place of residence for parents; clinical covariates for parents include obstetric antecedents, type of childbirth and previous abortion. Clinical covariates for babies include APGAR, gender, number of births at a time, weight, circumference of the head, and height.
Results/Conclusion:
The results revealed that Wei, Lin and Weissfeld Model (WLWM) fit the data well. The covariates age, abortion, gender, number, APGAR, weight and head were found to have a significant effect.
1. INTRODUCTION
The multiple events processes or processes that generate events repeatedly along the time are also known as the recurrent event processes [1]. Such processes are adapted to the repeated event data found in medicine and public health, where the number of events exhibited is relatively small for a larger number of processes. Multiple events are met in other domain such as social science, economics, manufacturing, insurance and reliability [2]. In multiple events studies, the number of events in distinct time intervals is termed as “counts”, the gaps are the times between successive event, while the “event intensity” is the conditional probability of new event, given the past event [1].
Cook and Lawless [1] discuss different multiplicative approach models such as the modulated Poisson model which consists of modeling the intensity processes given the history, and the Cox Models for ordered and unordered events. The interest in this study will be taken on the multiplicative model with the ordered events. Ordered events are based on the concept that the second event cannot occur before the first event, the third event cannot occur before the second event and so on. The models adapted to ordered events include the Andersen-Gill Model (AGM), the Wei, Lin and Weissfeld Model (WLWM) and the Prentice, Williams and Peterson Model (PWPM) [3].
The AGM known also as the counting process approach [4], assumes that all event types are indistinguishable and all events within the same subject are assumed to be independent [5]. Therneau [6] evokes a limitation of AGM of not allowing multiple events to occur at the same time. The WLWM is also known as the marginal risk sets model [7]. The WLWM assumes that events are unordered where each event has its own stratum and each data point appears in all strata. This allows an analysis of multiple events occurring at the same time. The PWPM also known as the conditional risk set model was proposed by Prentice, Williams and Peterson [8]. In PWPM, the set up of the dataset is the same as that of the AGM but the analysis is stratified by failure order [9]. The PWPM can potentially analyse time to each event from the previous event, this is known as the gap-time model. AGM, WLWM and PWPM have been alternatively used on bladder cancer data and on the hospitalisation and death data presented by Castañeda and Gerritse [10].
The WLWM will be used in this study for modeling the risk of infant at Kigali University Teaching Hospital from 01-January-2016 to 31-December-2016 with two events namely death or occurrence of a chronic disease or complication that is due to the type of the dataset where the events of interest can occur on the same day taken as a unit in this study.
Including the introduction, the study comprises four sections: Section 2 is the methodology of the study where the mathematical formulation of AGM, PWPM and WLWM is described. Section 3 gives the main results and interpretation and Section 4 gives conclusion.
2. METHODOLOGY
2.1. Mathematical Formulation of Cox Model with Multiple Events
Consider the time scale t, t > 0 and a sample of n individuals under study and let
Ni(t) denotes the number of events for individual i, i = 1, 2,..., n,
Ti1Ti2 denote the times of events for individual i,
Wij = Tij-Ti,j-1 denote the gaps or times between successive events of the individual i,
yi(t)’s denote the fixed or time-varying covarites.
Ni(t) is a counting process with intensity process
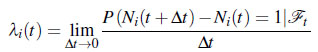 |
with Ft the history of events and covariates up to the time t [11]. The mean cumulative function (MCF) µi(t) and the corresponding rate of occurrence function ρi(t) are defined in [1] as:
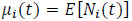 |
(1) |
and
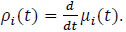 |
(2) |
or
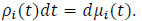 |
(3) |
Applying differentiation on both sides of (1) and using (3) yields:
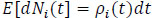 |
(4) |
Cook and Lawless [1] discuss different multiplicative approaches models such as the regression model for the rate function for both fixed and time-dependent covariates expressed by:
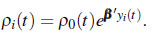 |
(5) |
and the regression model for the mean functions for the fixed covariates, expressed by
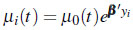 |
where 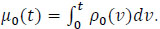
The second approach consisted of modeling the intensity process λi(t) given the history F, that is
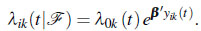 |
(6) |
The expression λ0k is the event specific baseline hazard for the kth event over time. Model (6) incorporate the AGM, WLWM and the PWPM according to the type of the dataset. Specifically Model (6) yield PWPM gap model of the form
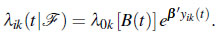 |
where B(t) = t-TN(t) is the time since the last event.
2.2. Likelihoods and Maximum Likelihood Estimation
The likelihoods constructions and maximum likelihood estimates for the multiplicative multiple events models are well developed in [1], and specifically [12], discussed a parametric based estimation for the rate function model; Lawless and Nadeau [13] addressed two ways of analyzing the rate function: The first one consists of specifying the distribution of the intensity process λi(t) such as for example a Poisson process when λi(t) = ρi(y), or a negative binomial process if 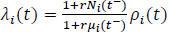 . In the second way, a distribution of the intensity process is not specified, this approach known as “robust” is potential to model means or variances [11].
. In the second way, a distribution of the intensity process is not specified, this approach known as “robust” is potential to model means or variances [11].
Assuming that two events cannot occur simultaneously in continuous time, let ]0, τi[, the interval of time in which the individual i is observed and ni the number of events of individual i along ]0, τi[, then the probability density function for the outcome ni along ]0, τi[ is given by:
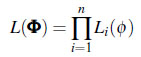 |
where
 |
(7) |
In (7), ϕ = (α, β); α is called a baseline parameter, τ = max(τ1, τ2,...τn) and:
 |
Using the relationship (4), the log-likelihood can be written:
 |
The maximum likelihood estimates are obtained by solving a system:
 |
(8) |
The numerical methods such as the Newton-Raphson method are used for solving the system (8). The adequacy of parameters is checked by finding the elements Iαα, Iαβ, Iβα and Iββ of the information matrix I and assume that as n → ∞,  [11].
[11].
2.3. Setup of Dataset in AGM, PWPM and WLWM
Numerical examples on the layout of dataset in the AGM, the PWPM and the WLWM are found in materials such as [14-21]. Assume that n is a maximum number of events per subject, and that τk, k = 1, 2,...n, are times to events per subject along the study time with range [0, T]. Under the AGM, All events are assumed to be in one stratum along the study time. The study time T is subdivided into intervals defined by the times to events such as 0 - τ1; τ1-τ2; τn-T, with event indicator for each time interval. The layout of dataset for PWPM is the same as for the AGM where for each interval corresponds a specific stratum, making the number of time intervals per subject equal to the number of strata per subject. The alternative PWPM based on gape time take 0 at lower bound of each interval per subject, the upper bound is given by the gaps or τk-τk-1, k = 1, 2,...,n; the first and the last intervals are respectively 0 - τ1 and T-τn. Like in PWPM, the kth time interval per subject in WLWM is in the kth stratum, k = 1, 2,...,n. In WLWM, the study time is subdivided into n + 1 intervals each with lower bound 0 and upper bound equal to the time to event, the first and the last intervals are respectively 0 - τ1 and 0 - T.
2.4. Dataset
The primary dataset of newborns at KUTH is recorded from 1st January to 31st December 2016 and a complete case analysis is considered. Two events per subject are of interest: death and occurrence of at least one chronic disease or complication. The chronic disease or complications recorded at KUTH are severe oliguria, severe prematurity, very low birth weight, macrosomia, severe respiratory distress, gastroparesis, hemolytic, trisomy, asphyxia and laparoschisis. Beside the event status and the time to an event, eleven covariates are of interest: demographic covariates that include the age and the place of residence for parents; clinical covariates for parents which include obstetric antecedents, type of childbirth and previous abortion. Clinical covariates for children include APGAR; gender, number of births at a time, weight, circumference of the head, and height, Table 1 describes the variables of interest.
| Variable Description Codes/Values/Unit | Variable Description Codes/Values/Unit | Variable Description Codes/Values/Unit |
|---|---|---|
| Variable | Description | Codes/Values/Unit |
| Age | Age of parent | 0 = under 20, 1 = 20 years old to 34 years old, 2 = 35 years old and above |
| Residence | Indicator of the residential area of a parent | 0 = rural, 1 = urban |
| Antecedents | Indicator on whether a new born is the first or not | 0 = Not the first new born, 1 = first newborn, |
| Abortion | Indicator on whether a parent aborted previously | 0 = not aborted, 1aborted once, 2 = aborted more than once |
| Childbirth | Type of childbirth | 0 = born using ventouse, 1 = born naturally, 2 = born after surgery |
| Gender | Gender of a newborn | 0 = female, 1 = male |
| Number | Indicator of the number of births at a time | 0 = singleton, 1 = multiple |
| APGAR | Score of appearance, pulse, grimaces, activity and respiration of a newborn | 0 = APGAR less than 4/10, 1 = APGAR from 4/10 to 6/10 to, 2 = APGAR greater or equal to 7/10 |
| Weight | Weight of a newborn | 0 = under 2500 g, 1 = 2500 g to 4500 g, 2 = above 4500 g |
| Head | Head circumference of a newborn | 0 below 32 cm, 1 = 32 cm to 36 cm, 2 = above 36 cm |
| Height | Height of a new born | 0 = below 46 cm, 1=46 cm to 54 cm, 2 = above 54 cm |
| Time | Time from recruitment to study termination | Days |
| Event | Indicator describing if death occurred during the study time or not | 0 = censored, 1 = dead |
| Indicator on the rank of records per subject | 1 = first record, 2 = second record |
The layout follows the indication provided by the WLWM, Table 2 gives the first 50 entries, the full dataset can be found via the authors of this article.
| No | Id | Age | Residence | Antecedents | Abortion | Childbirth | Gender | Number | Apgar | Weight | Head | Height | Tstart | Tstop | Event | N_events |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 39 | 0 | 1 | |
| 2 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 212 | 0 | 1 | |
| 3 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 196 | 0 | 1 | |
| 4 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 128 | 0 | 1 | |
| 5 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 335 | 0 | 1 | |
| 6 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 262 | 0 | 1 | |
| 7 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 214 | 0 | 1 | |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 228 | 0 | 1 | |
| 9 | 2 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 355 | 0 | 1 | |
| 10 | 1 | 1 | 1 | 0 | 2 | 1 | 0 | 2 | 0 | 1 | 1 | 0 | 25 | 0 | 1 | |
| 11 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 256 | 0 | 1 | |
| 12 | 2 | 0 | 1 | 0 | 2 | 0 | 1 | 2 | 0 | 1 | 1 | 0 | 179 | 0 | 1 | |
| 13 | 2 | 0 | 1 | 0 | 2 | 0 | 1 | 2 | 0 | 1 | 1 | 0 | 179 | 0 | 1 | |
| 14 | 2 | 0 | 1 | 0 | 2 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 179 | 0 | 1 | |
| 15 | 2 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 348 | 0 | 1 | |
| 16 | 1 | 1 | 0 | 1 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 305 | 0 | 1 | |
| 17 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 45 | 0 | 1 | |
| 18 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 129 | 0 | 1 | |
| 19 | 1 | 1 | 0 | 0 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 19 | 1 | 1 | 0 | 0 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 0 | 0 | 1 | 2 | |
| 20 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 137 | 0 | 1 | |
| 21 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 293 | 0 | 1 | |
| 22 | 2 | 1 | 0 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 70 | 0 | 1 | |
| 25 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 25 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 2 | |
| 23 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 218 | 0 | 1 | |
| 24 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 260 | 0 | 1 | |
| 26 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 24 | 0 | 1 | |
| 27 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 16 | 0 | 1 | |
| 28 | 1 | 0 | 1 | 0 | 2 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 318 | 0 | 1 | |
| 29 | 2 | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 29 | 2 | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 6 | 1 | 2 | |
| 30 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 249 | 0 | 1 | |
| 31 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 311 | 0 | 1 | |
| 32 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 357 | 0 | 1 | |
| 33 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 1 | 1 | 0 | 232 | 0 | 1 | |
| 34 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 356 | 0 | 1 | |
| 35 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 140 | 0 | 1 | |
| 36 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 2 | 0 | 272 | 0 | 1 | |
| 37 | 2 | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 203 | 0 | 1 | |
| 38 | 1 | 1 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 2 | 0 | 0 | 235 | 0 | 1 | |
| 39 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 305 | 0 | 1 | |
| 40 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 263 | 0 | 1 | |
| 41 | 2 | 0 | 0 | 2 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 192 | 0 | 1 | |
| 42 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 248 | 0 | 1 | |
| 43 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 43 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 4 | 1 | 2 | |
| 44 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 254 | 0 | 1 | |
| 45 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 333 | 0 | 1 | |
| 46 | 1 | 1 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 1 | 1 | 0 | 39 | 0 | 1 |
3. RESULTS AND INTERPRETATION
Model is implemented by using STATA package, version 14 and the dataset on infant mortality at KUTH with a portion given in Table 2. The WLWM is used since death can occur without a previous chronic disease or complication and the two events could occur at the same time per subject.
Tables 3, 4 and 5 present the estimates of the hazard ratios of the unadjusted WLWM with ties handling by Breslow, Efron and Cox approaches, respectively. The results in the later two approaches are not far from that of the default method (Breslow). Significant differences in levels are observed for the same covariates in all approaches for the age, abortion, gender, number, APGAR, weight and head where p-values are less or equal to.
| Covariate (reference) | Level | Hazard Ratio | Std. Err | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.277 | 0.997 | -3.570 | p < 0.001 | [0.137; 0.560] |
| 35 years old and above | 0.395 | 0.157 | -2.330 | 0.020 | [0.181; 0.863] | |
| Residence (Rural) | Urban | 0.847 | 0.139 | -1.020 | 0.309 | [0.614; 1.167] |
| Antecedents (Not 1st newborn) | 1st new born | 0.806 | 0.157 | -1.100 | 0.270 | [0.550; 1.182] |
| Abortion (Not aborted) | Aborted once | 1.405 | 0.398 | 1.200 | 0.231 | [0.806; 2.448] |
| Aborted more than once | 0.479 | 0.161 | -2.190 | 0.028 | [0.248; 0.925] | |
| Childbirth (Ventouse) | Natural | 0.873 | 0.491 | -0.240 | 0.808 | [0.290; 2.627] |
| Surgery | 1.115 | 0.613 | 0.200 | 0.843 | [0.380; 3.274] | |
| Gender (Female) | Male | 1.740 | 0.296 | 3.260 | 0.001 | [1.247; 2.429] |
| Number (Singleton) | Multiple | 0.409 | 0.131 | -2.790 | 0.005 | [0.218; 0.766] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.377 | 0.112 | -3.300 | 0.001 | [0.211; 0.673] |
| 7/10 and above | 0.130 | 0.036 | -7.460 | p < 0.001 | [0.076; 0.222] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.250 | 0.068 | -5.070 | p < 0.001 | [0.146; 0.427] |
| Above 4500 g | 0.442 | 0.285 | -1.270 | 0.206 | [0.125; 1.565] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.456 | 0.128 | -2.800 | 0.005 | [0.263; 0.789] |
| Above 36 cm | 0.290 | 0.219 | -1.640 | 0.102 | [0.066; 1.278] | |
| Height (Below 46 cm) | 46 cm to 54 cm | 0.894 | 0.276 | -0.360 | 0.716 | [0.488; 1.637] |
| Above 54 cm | 1.670 | 1.264 | 0.680 | 0.498 | [0.379; 7.361] |
| Covariate (reference) | Level | Hazard Ratio | Std. Err. | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.230 | 0.083 | -4.080 | p < 0.001 | [0.114; 0.466] |
| 35 years old and above | 0.324 | 0.129 | -2.840 | 0.005 | [0.149; 0.706] | |
| Residence (Rural) | Urban | 0.831 | 0.137 | -1.120 | 0.261 | [0.602; 1.147] |
| Antecedents (Not 1st newborn) | 1st newborn | 0.756 | 0.149 | -1.420 | 0.156 | [0.513; 1.113] |
| Abortion (Not aborted) | Aborted once | 1.393 | 0.396 | 1.170 | 0.244 | [0.798; 2.430] |
| Aborted more than once | 0.452 | 0.154 | -2.340 | 0.020 | [0.232; 0.880] | |
| Childbirth (Ventouse) | Natural | 0.736 | 0.408 | -0.550 | 0.580 | [0.249; 2.179] |
| Surgery | 0.921 | 0.499 | -0.150 | 0.880 | [0.319; 2.661] | |
| Gender (Female) | Male | 1.823 | 0.312 | 3.520 | p < 0.001 | [1.304; 2.549] |
| Number (Singleton) | Multiple | 0.324 | 0.106 | -3.430 | 0.001 | [0.170; 0.617] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.214 | 0.065 | -5.090 | p < 0.001 | [0.118; 0.387] |
| 7/10 and above | 0.070 | 0.020 | -9.520 | p < 0.001 | [0.041; 0.121] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.231 | 0.063 | -5.340 | p < 0.001 | [0.135; 0.395] |
| Above 4500 g | 0.412 | 0.269 | -1.360 | 0.174 | [0.115; 1.479] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.422 | 0.119 | -3.060 | 0.002 | [0.243; 0.734] |
| Above 36 cm | 0.246 | 0.187 | -1.840 | 0.065 | [0.055; 1.093] | |
| Height (Below 46 cm) | 46 cm to 54 cm | 0.917 | 0.285 | -0.280 | 0.781 | [0.499; 1.687] |
| Above 54 cm | 1.692 | 1.283 | 0.690 | 0.488 | [0.383; 7.476] |
| Covariate (reference) | Level | Hazard Ratio | Std. Err. | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.193 | 0.085 | -3.730 | p < 0.001 | [0.081; 0.458] |
| 35 years old and above | 0.267 | 0.128 | -2.760 | 0.006 | [0.104; 0.682] | |
| Residence (Rural) | Urban | 0.766 | 0.150 | -1.360 | 0.175 | [0.521; 1.126] |
| Antecedents (Not 1st newborn) | 1st newborn | 0.763 | 0.185 | -1.120 | 0.264 | [0.475; 1.226] |
| Abortion (Not aborted) | Aborted once | 1.404 | 0.453 | 1.050 | 0.293 | [0.746; 2.643] |
| Aborted more than once | 0.378 | 0.152 | -2.420 | 0.015 | [0.172; 0.830] | |
| Childbirth (Ventouse) | Natural | 0.732 | 0.481 | -0.470 | 0.635 | [0.202; 2.653] |
| Surgery | 1.016 | 0.654 | 0.030 | 0.980 | [0.288; 3.590] | |
| Gender (Female) | Male | 1.991 | 0.405 | 3.390 | 0.001 | [1.336; 2.966] |
| Number (Singleton) | Multiple | 0.218 | 0.111 | -3.000 | 0.003 | [0.080; 0.589] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.080 | 0.042 | -4.810 | p < 0.001 | [0.029; 0.224] |
| 7/10 and above | 0.021 | 0.011 | -7.840 | p < 0.001 | [0.008; 0.056] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.236 | 0.070 | -4.850 | p < 0.001 | [0.131; 0.423] |
| Above 4500 g | 0.378 | 0.257 | -1.430 | 0.153 | [0.100; 1.436] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.391 | 0.119 | -3.100 | 0.002 | [0.216; 0.708] |
| Above 36 cm | 0.212 | 0.171 | -1.920 | 0.055 | [0.043; 1.033] | |
| Height (Below 46 cm) | 46 cm to 54 cm | 0.828 | 0.283 | -0.550 | 0.582 | [0.423; 1.620] |
| Above 54 cm | 1.706 | 1.351 | 0.670 | 0.500 | [0.361; 8.060] |
The adjusted WLWM with Breslow74, Efron77 and Cox72 methods of ties handling is summarised in Tables 6, 7 and 8 and the results are not critically different.
| Covariate (reference) | Level | Hazard ratio | Std. Err. | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.307 | 0.107 | 3.380 | 0.001 | [0.155; 0.609 ] |
| 35 years old and above | 0.472 | 0.179 | -1.980 | 0.047 | [0.225; 0.992] | |
| Abortion (Not aborted) | Aborted once | 1.482 | 0.406 | 1.430 | 0.152 | [0.866; 2.537] |
| Aborted more than once | 0.541 | 0.175 | -1.900 | 0.057 | [0.287; 1.019] | |
| Gender (Female) | Male | 1.672 | 0.280 | 3.070 | 0.002 | [1.204; 2.321] |
| Number (Singleton) | Multiple | 0.401 | 0.128 | -2.860 | 0.004 | [0.214; 0.750] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.414 | 0.119 | -3.080 | 0.002 | [0.236; 0.726] |
| 7/10 and above | 0.144 | 0.038 | -7.350 | p < 0.001 | [0.086; 0.242] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.238 | 0.060 | -5.650 | p < 0.001 | [0.144; 0.391] |
| Above 4500 g | 0.447 | 0.284 | -1.270 | 0.205 | [0.129; 1.550] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.420 | 0.100 | -3.660 | 0.000 | [0.264; 0.669] |
| Above 36 cm | 0.284 | 0.210 | -1.700 | 0.089 | [0.067; 1.211] |
| Covariate (reference) | Level | Hazard Ratio | Std. Err. | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.262 | 0.092 | -3.810 | p < 0.001 | [0.132; 0.522] |
| 35 years old and above | 0.407 | 0.155 | -2.360 | 0.018 | [0.193; 0.859] | |
| Abortion (Not aborted) | Aborted once | 1.487 | 0.408 | 1.440 | 0.149 | [0.868; 2.546] |
| Aborted more than once | 0.520 | 0.170 | -2.000 | 0.046 | [0.274; 0.987] | |
| Gender (Female) | Male | 1.764 | 0.297 | 3.370 | 0.001 | [1.268; 2.453] |
| Number (Singleton) | Multiple | 0.308 | 0.101 | -3.580 | p < 0.001 | [0.162; 0.586] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.249 | 0.073 | -4.730 | p < 0.001 | [0.140; 0.442] |
| 7/10 and above | 0.081 | 0.022 | -9.400 | p < 0.001 | [0.048; 0.137] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.222 | 0.057 | -5.910 | p < 0.001 | [0.135; 0.366] |
| Above 4500 g | 0.430 | 0.276 | -1.310 | 0.189 | [0.122; 1.512] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.388 | 0.093 | -3.940 | p < 0.001 | [0.243; 0.622] |
| Above 36 cm | 0.235 | 0.175 | -1.940 | 0.052 | [0.054; 1.014] |
| Covariate (reference) | Level | Hazard Ratio | Std. Err. | z | P > z | 95% Conf. Int. |
|---|---|---|---|---|---|---|
| Age (Under 20 years old) | 20 to 34 years old | 0.218 | 0.094 | -3.520 | p < 0.001 | [0.094; 0.509] |
| 35 years old and above | 0.341 | 0.157 | -2.340 | 0.019 | [0.138; 0.841] | |
| Abortion (Not aborted) | Aborted once | 1.479 | 0.459 | 1.260 | 0.208 | [0.804; 2.719] |
| Aborted more than once | 0.424 | 0.161 | -2.260 | 0.024 | [0.201; 0.892] | |
| Gender (Female) | Male | 1.886 | 0.374 | 3.200 | 0.001 | [1.278; 2.783] |
| Number (Singleton) | Multiple | 0.214 | 0.108 | -3.050 | 0.002 | [0.079; 0.576] |
| APGAR (Below 4/10) | 4/10 to 6/10 | 0.098 | 0.050 | -4.550 | p < 0.001 | [0.036; 0.267] |
| 7/10 and above | 0.026 | 0.012 | -7.680 | p < 0.001 | [0.010; 0.066] | |
| Weight (Under 2500 g) | 2500 g to 4500 g | 0.213 | 0.057 | -5.730 | p < 0.001 | [0.125; 0.361] |
| Above 4500 g | 0.364 | 0.245 | -1.500 | 0.134 | [0.097; 1.364] | |
| Head (Below 32 cm) | 32 cm to 36 cm | 0.349 | 0.090 | -4.080 | p < 0.001 | [0.211; 0.579] |
| Above 36 cm | 0.199 | 0.160 | -2.020 | 0.044 | [0.042; 0.957] |
The adjusted model by default (Breslow) suggests that the risk of death or attracting a chronic disease or complication of babies whose parents are from 20 years and 34 years old is 0.307 times that of babies whose parents are under 20 years old (95% CI:0.155-0.609, p = 0.001). The risk of death or attracting a chronic disease or complication of babies whose parents aborted more than once previously is 0.541 times that of babies whose parents did not aborted previously (95% CI:0.287-1.019, p = 0.057). The risk of death or attracting a chronic disease or complication of babies whose parents are 35 years old and above is 0.472 times that of babies whose parents are under 20 years old (95% CI:0.225-0.992, p = 0.047). The risk of death or attracting a chronic disease or complication for male babies is 1.672 times that of female babies (95% CI:1.204-2.321, p = 0.002). The risk of death or attracting a chronic disease or complication of multiple babies is 0.401 times that of singleton babies (95% CI:0.214-0.750, p = 0.004) The risk of death or attracting a chronic disease or complication for babies whose APGAR range from 4/10 to 6/10 is 0.414 times that of babies whose APGAR is below 4/10 (95% CI:0.236-0.726, p = 0.002). The risk of death or attracting a chronic disease or complication for babies whose APGAR range from 7/10 to 10/10 is 0.144 times that of babies whose APGAR is below 4/10 (95% CI:0.086-0.242, p < 0.001). The risk of death or attracting a chronic disease or complication for babies whose weight range from 2500 g to 4500 g is 0.238 times that of babies whose weight is below 2500 g (95% CI:0.144-0.391, p < 0.001). The risk of death or attracting a chronic disease or complication for babies whose circumference of head range from 32 cm to 36 cm is 0.420 times that of babies whose circumference of head is is below 32 cm (95% CI:0.264-0.669, p < 0.001). The risk of death or attracting a chronic disease or complication for babies whose circumference of head is above 36 cm is 0.284 times that of babies whose circumference of head is is below 32 cm (95% CI:0.067-1.211, p = 0.067).
CONCLUSION
This paper reviewed different multiplicative multiple events regression models of the time to event survival data namely the mean function regression model, the rate function regression model and the intensity process regression model. The intensity process regression model incorporates the popular models such as Andersen- Gill Model (AGM), Wei, Lin and Weisfeld Model (WLWM) and the Prentice, Williams and Peterson Model (PWPM) following on the layout of the dataset. It was found that data collected at Kigali University Teaching Hospital for 2117 newborns during 365 days of the year 2016 follows the conditions of the WLWM.
The results of the unadjusted WLWM by Breslow, Efron and Cox approaches of ties handling revealed significance on the age of female parents, information on previous abortion, gender of newborn, number of newborns at a time, APGAR, weight of a newborn and the circumference of the head of a newborn. The results of adjusted WLWM by Breslow, Efron and Cox are not critically different. The default approach (Breslow) indicated that the risk of death or attracting a chronic disease or clinical complication of infant is higher in male babies as compared to female babies; it is lower for babies whose parents are from 20 to 34 years old and above 34 years old as compared to babies whose parents are under 20 years old. Babies whose APGAR fall in intervals 4/10 to 7/10 and 7/0 to 10/10 were found to have a better survival outcome than those born with APGAR less than 4/10. Babies with normal weight and overweight were found to have a lower risk as compared to underweight babies. Babies with a normal circumference of head and those with large circumference of head were found to survive better than babies with the relatively small head.
Analysis was limited to only 11 variables. Unavailable variables concerning parents that could improve models are, for example, demographic variables such as education level, employment and income, behavioral variables such as smoking habit, alcohol consumption and dietary and physio-therapeutic variables such as sports activity level. These variables are not recorded in registry at KUTH.
The future work will consist of testing parametric distribution that could be adapted to the infant mortality at KUTH. The suitable parametric model will be fitted by using appropriate parametric regression model.
ETHICAL APPROVAL AND CONSENT TO PARTICIPATE
We were granted permission to record dataset from registry of the Kigali University Teaching Hospital.
HUMAN AND ANIMAL RIGHTS
No animals / humans were used for the studies that are bases of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This work was supported through the DELTAS Africa Initiative. The DELTAS Africa Initiative is an independent funding scheme of the African Academy of Sciences (AAS)’s Alliance for Accelerating Excellence in Science in Africa (AESA) and supported by the New Partnership for Africa’s Development Planning and Coordinating Agency (NEPAD Agency) with funding from the Wellcome Trust [grant 107754/Z/15/Z- DELTAS Africa Sub-Saharan Africa Consortium for Advanced Biostatistics (SSACAB) programme] and the UK government. The views expressed in this publication are those of the author(s) and not necessarily those of AAS, NEPAD Agency, Wellcome Trust or the UK government.


