All published articles of this journal are available on ScienceDirect.
Spatial Modelling of Under-five Mortality in Lesotho with Reference to 2014 Demographic and Health Surveillance Dataset
Abstract
Background:
Lesotho is the country located in the Sub-Saharan region of Africa countries where under-five mortality (U5M) is still a big issue due to some significant social and demographic risk factors. Hence, the investigation of some social and demographic factors that are associated with the U5M, is a critical problem that needs due consideration.
Methods:
This study used the 2014 Lesotho Demographic and Health Survey (LDHS) that had a sample of over 9000 representative households. Individually, data consisting of a nationally representative sample of 9,543 households in the 2014 Lesotho Demographic and Health Survey were analysed. The Random Walk second-order (RW2) model was adopted for analysis. Maps construction and modelling were done through the spatially structured and unstructured random effects using the Gaussian Markov Random Field and a zero-mean Gaussian process, respectively. The full Bayesian inference was adopted to produce the results using the Integrated Nested Laplace Approximation (INLA) function in R-software.
Results:
In this study, age at death of an under-five child was found to have a linear association with the U5M in Lesotho. The non-stationary models outperform the stationary models. The low-risk pattern was found in the north of Lesotho, and the highest risk occurs in the centre through the south, east, west, southeast, and northwest. Breastfeeding has contributed significantly to under-five mortality to most of Lesotho districts.
Conclusion:
This study adopted the newly developed statistical models to model and mapped the U5M in Lesotho. The full Bayesian inference was used to produce the results using R-INLA package. The findings from this study can help introduce new policies that will help reduce disparity in Lesotho.
1. INTRODUCTION
Under-five Mortality (U5M) is the probability of a child dying between birth and exactly five years of age expressed per 1000 live birth [1]. In the whole world, reducing child death as well as improving child health are significant concerns of the development agencies and the international public health communities [2]. Most of the under-five deaths are due to infectious diseases and injuries; and these deaths reflect the limited access of under-five children and communities to essential health interventions such as vaccination, medication of contagious illnesses, adequate nutrition, and clean water and sanitation [3].
Under-five mortality is a serious public health issue in Lesotho [4]. Lesotho is in the SDG region, which aims to reduce the mortality rate to an average of 25 death per 1000 live births under the sustainable development goal before 2030 [5]. Still, this goal seems to be impossible due to ups and downs of the death rate of under-five child death in Lesotho due to social and demographics factors that are associated with child survival. Previously, there has been little Statistical work concerning under-five mortality in Lesotho, especially using the recently developed spatial mapping models. In this paper, we followed the Bayesian techniques, which has numerous advantages over frequentist Statistics in terms of inferring the model parameters of interest. When the covariates are spatially indexed, the non-spatial and spatial stationary regression tends to give inadequate predictions due to ignoring the spatial dependences. If the assumption of uncorrelated residuals is violated, a spatially varying coefficient model is added to account for the association through a decreasing function of distance and perhaps direction between observed locations [6]. Taking into consideration the residuals uncertainty in our model, especially when we are studying complexity due to potential space-varying and dependent relationships between the predictors and the response, can improve the inference. It also increases prediction accuracy and precision; this is further discussed by Cressie, N et al., 2009 [7]. The Geographically Weighted Regression (GWR) detailed by Brunsdon, C., 2002 [8] and the hierarchical modelling techniques using Bayesian Spatially Varying Coefficient Process (BSVCP) discussed by Assunçao, R.M., 2003 [9] are the commonly used methods to analyse such data. In the previous studies [6, 8, 10], it has been shown that BSVCP model has outperformed the GWR model in the estimation and validation of results.
The study by Hu et al. 2011 [11] used the hierarchical Bayesian model to map the distribution of under-five mortality in the Wenchuan at the township scale. The study confirmed that the Bayesian approach outperforms other methods in its smoothing effects as well as in the exploration of the different aspects of the patterns. Li et al. 2019 [12] used binomial likelihood with fixed effects for the urban/rural stratification to account for the complex design. They produced yearly estimates for subnational areas in Kenya over the period 1980 - 2014 using the KDHS data set. They carry out smoothing using Bayesian hierarchical models with continuous spatial and temporally discrete components. Their study discovered that there had been a sharp decline in the U5M rate in the period 1980 - 2014, but significant variability in the estimated subnational rates remains. Luchemo, O.E., 2017 [13] used data from the Kenya AIDS indicator survey for 2007, which was stratified in two-stage cluster sampling design, he started by fitting the univariate standard logistic model between every single covariate with the outcome variable (HIV and HSV-2 status). The covariates that showed the significant effect on the outcome variable were applied to 8 models he created, of which four were stationary. The other 4 were spatially varying coefficient models. His study showed that spatially varying coefficient models outperform the stationary models, and he also presented his results on the choropleth maps to show how each covariate affects each outcome variable, which is distributed across Kenya. However, the above first two studies and other studies in the literature use the likelihood with fixed effects for urban/rural stratification to account for complex design. This study follows the Bayesian modelling that uses structured and unstructured random effect for modelling and mapping. Our objective in this paper is to perform the spatial modelling analysis while relaxing the stationarity and linearity assumptions through Bayesian spatially varying coefficient process and random walk of order 2, respectively, to model the Lesotho 2014 Demographic and health survey data set.
2. DATA AND METHODS
2.1. Data Source and Variables
In this study, we used the dataset from Lesotho Demographic and Health Survey (LDHS) collected in 2014. Rutstein, S.O., 2000 [14] states that the Demographic and Health Survey (DHS) is said to be one of the world’s largest surveys with birth histories of women of reproductive ages from which infant and child mortality rates are derived. The survey was conducted in union with the Bureau of Statistics of Lesotho and Inner-City Fund (ICF) Macro that provided technical assistance. The fieldwork for 2014 from 22 September, 2014 through 7 December, 2014. These LDHS followed a two-stage sample design and was planned to permit estimates of key indicators at the national level as well as in urban and rural areas, and each of Lesotho’s ten districts. In the first stage, clusters consisting of enumeration areas were selected from 2006 population Census areas for 2014, comprising of 400 clusters (306 and 284 in the rural). The second stage included a systematic sampling of households. A three-model questionnaire for DHS was taken into consideration, which comprised of men, women, and households. The number of women aged 15-49 interviewed in 2014 LDHS was 6621 out of 6818 eligible. The data used in this study comprised both categorical and continuous covariates. The variables were categorized into two groups, namely: demographic and social characteristics. From the initial analysis, it was observed that the level of education, place of residence, current breastfeeding, and the number of children 5 or under were found to have an association with the child status, as shown in Table 3.
2.2. Statistical Model
The binary logistic regression model is a statistical technique that is usually used when there are one or more predictor variables; and a response variable that is measured with a dichotomous (binary) structure [15]. Initially, a non-spatial data analysis was carried out using a binary logistic regression model to describe the relationship between the binary variable of interest (Child is dead coded as 1 and otherwise 0) variables and other covariates. The association was considered at a 5% level of significance, as shown in Table 3. Let yij be the child j status in district i, with yij = 0, if a child is dead and 1 otherwise. Thus, a region, location or similar structure contains a cluster of observations. In this study, we assume that the response variable yij is univariate Bernoulli distributed, that is yij|pij~Benoulli(pij). The p continuous independent variables are contained in the vector Xij = (xi1, xi2,..., xip)' while Wij = (wi1, wi2,..., wir)' contain r categorical independent random variables.
In most cases, smoothing techniques play a vital role in the non-parametric regression approach [16]. The penalized (P-spline) regression proposed by, for example, Eilers, P.H. et al., 1996 [17], has been extensively used. In this case, the polynomial spline is assumed to approximate the effect of continuous covariates. Here, the P-spline model is linked with the Random Walk (RW) prior to the Bayesian framework, and the Bayesian inference for the P-spline model is used via the R-INLA package. They assume RW prior for an equally spaced location such that yi~N(f(xi, σ2ϵ) and without the loss of generality, the observation is assumed to be ordered as x1 < x2 ... < xn and define di = d for i = 1,..., n - 1 where d is some constant. To understand how this RW prior brings smoothness to the fitted function, we consider the full conditional distribution p(f(xi)|f-i) where f-i denotes all the elements in f except f(xi). The distribution turns out to be normal with a mean that is a weighted average of function values that come from the neighbours of xi. The full conditional distribution of the second-order (RW2) priors is Eq.(1)
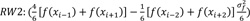 |
(1) |
where we can see the conditional independence properties of the two models: mean of f(xi) only depends on its second-order neighbours and is conditionally independent of those outside the neighbourhood. This local structure applies smoothness to the estimated function. The areal data is a type of vital spatial data, where observations are related to a geographic region with adjacency information. In order to smooth the data, in this case, a neighbourhood structure is constructed. In most cases, two regions are said to be neighbours if they share a common border, but other ways to define neighbours are possible. Under RW models, a Gaussian increment is defined between neighbouring regions i and j as (Eq.2)
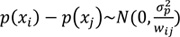 |
(2) |
where xi and xj represent the centroids of the regions, and wij are the positive and symmetric weights. We can let wij = 1 if we believe region i equally depends on its neighbours, or wij be, for example, the inverse Euclidean distance between the region centroids if we think the neighbours somehow contribute differently. Assuming the increments are independent, the resulting density of f = (f (xi)...f(xn))' is again multivariate normal with mean zeroes and precision matrix σ-2fQ where Q is the highly sparse matrix that has entries (Eq.3)
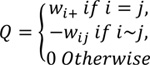 |
(3) |
where
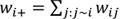 the summation over neighbours of region i. Since the sum of each row is zero, Q is of singular rank n-1. We can show that the full conditional distribution prior to p(xi) is normal (Eq.4)
the summation over neighbours of region i. Since the sum of each row is zero, Q is of singular rank n-1. We can show that the full conditional distribution prior to p(xi) is normal (Eq.4)
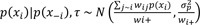 |
(4) |
where the conditional mean of p(xi) depends on its neighbouring nodes p(xj) through weights wij, and its conditional variance depends on weight sum wi+. We call this prior to a Besag model because it is a special case of the intrinsic autoregressive models introduced by Besag, J. et al., 1995 [18].
2.3. Parameter Estimation
In this study, we used the fully Bayesian estimation technique where parameters were assigned prior distributions. Based on the information of various research sources [19-21], more suitable user-defined hyper priors have been given using suitable expressions in INLA. Specifically, the non-informative normal distribution prior was used for the fixed effects, while a random walk model of order 2 was used for the continuous covariate age at the death of an under-five child. The spatial components were the CAR model for the structured random effects [12]. The posterior distribution is obtained after combining the prior distribution with the observed data. In this paper, we used the fully Bayesian strategy, and the implementation to obtain inferences for the latent Gaussian models was performed through the R software using the INLA function.
2.4. The Criteria for Model Selection
The models were compared using the Watanabe-Akaike Information Criterion (WAIC). The best model is the one with the smallest WAIC. The WAIC is obtained as WAIC = pw1 + pw2, where pw1 indicates the expected log pointwise posterior density for a new dataset and pw2 denotes the effective number of parameters [20].
2.5. Application/Data Analysis
The following models were used to investigate and understand the effect of the observed covariates and unobserved effects on the distribution of under-five mortality with reference to 2014 LDHS data using INLA library in R.
Model 1
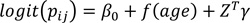 |
Model 2
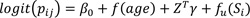 |
Model 3
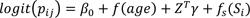 |
Model 4
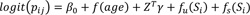 |
Model 5
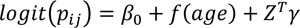 |
Model 6
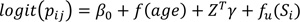 |
Model 7
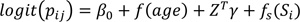 |
Model 8
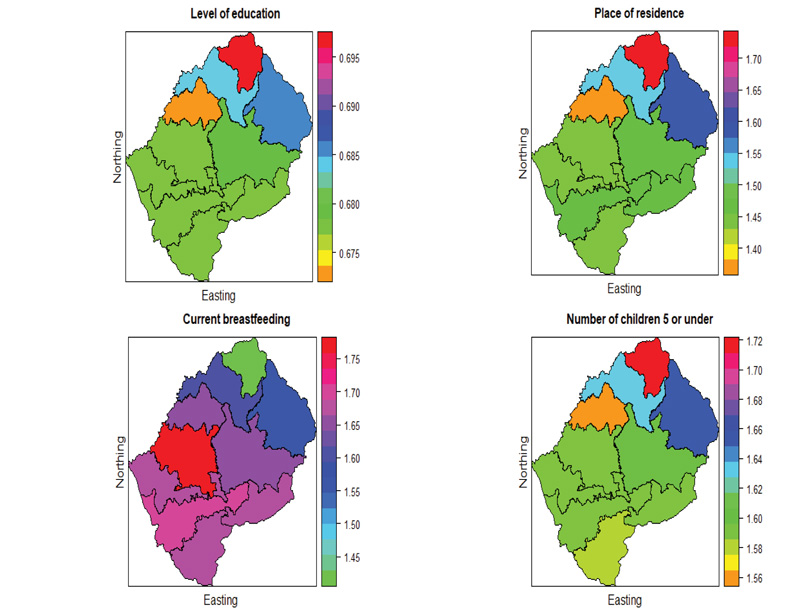
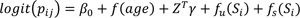 |
Where
• βO is the intercept representing the logit prevalence rate, where all covariates have zero value.
• f(age) represents a function of age. Here, age is a continuous predictor model with a non-linear smooth function: the RW2.
• Z Tγ represents the vector of categorical predictors for child j living in district i with γ represents the regression coefficient for the spatial model.
• fu(Si) represent spatially unstructured random effect, which caters to the unobserved predictors that are inherited within districts specified by the identically and independently distributed (iid) normal distribution.
• fs(Si) represents spatially structured random effect, which allows for some unobserved predictors which differ spatially among districts, specified by the Conditional Autoregressive Regression (CAR) model.
Model 1: We assume fixed categorical predictors with linear effects on the dependent variable. In this model, age is modelled as having a non-linear effect on the response; this agrees with the results from [20, 21] who supports modelling age with non-linear smoothing prior. Model one is a non-spatial model; here, the risk is modelled independently.
Model 2: This is an additive model that assumes the linear effect of the categorical predictors, the non-linear effect of the continuous predictor.
Model 3: This model explores the effect of the linear predictors in Model 1 above, non-linear predictor and spatially structured random effect, which accounts for any unobserved predictions which differ spatially among districts, specified by CAR model.
Model 4: This model studies the convolution of spatially structured and spatially unstructured random effects specified by the CAR model and the iid normal distribution respectively while taking into account the non-linear effect of age and linear effect of categorical predictors.
Models 5-8 They are similar to models 1 to 4, respectively. The only difference is that the regression coefficients γ in these models are assumed to violate or relax the stationarity assumption and are assigned the CAR priors to allow for spatially varying covariate effects.
3. RESULTS
3.1. Model Selection
In Table 1, there is Watanabe-Akaike Information Criterion (WAIC) for the four separately fitted models for U5M under the stationary covariate effect assumption are displayed. The four models were assumed to have stationary coefficients. Model 3 has the smallest WAIC of 880.63; hence it is preferable. Table 2 shows the WAIC for the four spatially varying coefficient models. From Table 2, we can see that model 8 has the smallest WAIC of 853.04. Therefore, this model provides the best fit for U5M. We, therefore, present and discuss the results based on model 3 under stationarity and on model 8 to allow covariates to vary spatially by the CAR model. Model 3 captures the structured effects, but model 8 captures both the structured and unstructured random effects on U5M.
| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| pw1 | 4.97 | 5.45 | 7.72 | 3.09 |
| pw2 | 966.71 | 881.34 | 872.93 | 883.79 |
| WAIC | 971.68 | 886.79 | 880.63 | 886.88 |
| Model 5 | Model 6 | Model 7 | Model 8 | |
|---|---|---|---|---|
| pw1 | 11.62 | 29.12 | 96.42 | 53.65 |
| pw2 | 910.01 | 824.36 | 900.87 | 799.39 |
| WAIC | 921.63 | 853.48 | 997.29 | 853.04 |
Table 3 shows that the odds of death for children who were not breastfed are 4.6 (95%: 3.16;6.69) times the odds of death for children who were breastfed, and the difference is statistically significant since 95% does not include one (p-value < 0.001). Children who reside in the urban area has better odds of surviving 0.697 (95% 0.50;0.98) less than the odds of those from the rural area, and the difference is statistically significant since (p-value < 0.036). Children with mothers with secondary and higher education have lower odds of 0.808 less then the odds of children with mothers with none and primary education, and the difference is statistically significant (p-value <0.008). More than two children aged below 5 in the household contribute to under-five child mortality with the odds of 2.11 (95%: 1.87;4.5) times the odds for children who are less than two, the difference is statistically different (p-value < 0.001). Therefore, in this data analysis, it is shown that level of education, place of residence, current breastfeeding, and the number of children 5 or under were found to have an association with the child survival status as shown in Table 1. In this case, the child age at death has a nonlinear effect on the child survival status, hence its continuous form (mean = 4.43 and std. Deviation = 6.833 for 2004; mean = 5.27 and std. Deviation = 8.215 for 2009; and mean = 4.88 and std. Deviation = 7.663 for 2014). Hence, these variables from no spatial regression (Model 1) are investigated using the spatial model in the preceding sections of this paper.
All the proposed covariates were found to be associated with the U5M, as shown in Table 4. The odds of dying for under-five children from mothers who had secondary and higher education level was statistically significantly less than the odds of dying for children from mothers with none or primary education (OR=0.38, 95% CI: 0.26, 0.50). The odds of under-five mortality for children who were breastfed are 0.38 times for those who were not breastfed (OR=0.38, 95% CI: 0.17, 0.59). Children who were staying in urban areas had statistically significantly better odds of surviving than those living in rural areas (OR = 0.27, 95% CI: 0.16, 0.39). The odds of dying for a child below 5 years old if they were less than two in the household, was statistically significantly less than those who were two or more in the household (OR = 0.38, 95% CI: 0.25, 0.52). Fig. (1) shows the choropleth maps of the risk-based on model 3, the standard error and the associated 95% credible interval. From these maps, we can observe that Butha-Buthe district (shown by orange colour) and Mokhotlong (shown by lime colour) were predicted to have the smallest risk pattern of U5M and the highest risk pattern was found in Mafikeng district (indicated by red colour). Generally, the low-risk pattern of U5M occurs in the North of Lesotho, and the highest occurs in the central, South, East, West, South-East, and North-West.
3.2. Spatially Varying Effect
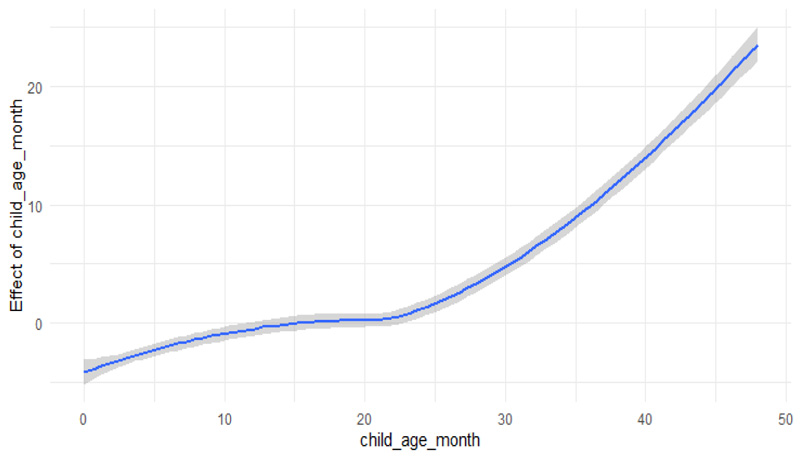
The choropleth maps in Fig. (3) suggest that the effect of some of the covariates indeed do differ spatially. The effects of education, type of residence, and the number of children five or under on U5M are more in Butha-Buthe (shown in red colour) and less in Berea (shown in orange), respectively, but the current breastfeeding is very low in Butha-Buthe (shown in green colour) and high in Maseru (shown in red colour). The effect of proposed covariates is similar in almost six districts (Quthing, Mohale’s Hoek, Mafikeng, Maseru, Thaba-Tseka and Qacha’s Neck). Furthermore, current breastfeeding has more effect on U5M from central to almost seven districts located in the South, South-East, South-West (indicated in red and maroon colours).
3.3. The Non-linear Effect of Age
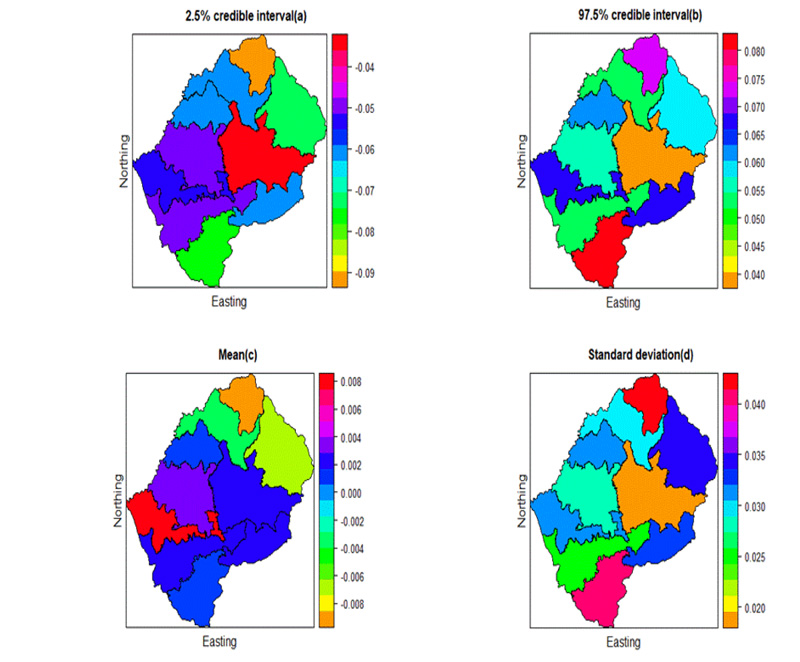
Fig. (2) gives the posterior mean of the smooth function, estimating the effect of age as a non-linear effect together with its 95% confidence interval. From the figure, there is evidence that the impact of age at death on U5M has positive and negative implications. The effect is linear from birth until 20 months and increases after 20 months toward 50 months. Hence, the higher child mortality is associated with child age for more than 20 months children. This increasing of U5M with rising age could be a result of nutrient scarcity in their diet, which may render them vulnerable to many infectious and other diseases than those below 20 months who were still likely to be breastfed.
| Variable | Std Error | P-value | OR (95% CI) |
|---|---|---|---|
| Demographic characteristics: | |||
| Place of residence (ref Rural) | 1 | ||
| Urban | 0.172 | 0.036 | 0.697(0.498;0.976) |
| Age of Household head (ref Less than 34 years) | 1 | ||
| More than 34 years | 0.156 | 0.476 | 0.985(0.659;1.215) |
| Sex of child (ref Male) | 1 | ||
| Female | 0.141 | 0.315 | 1.152(0.874;1.520) |
| Birth order (ref Less than 2 births) | 1 | ||
| More than 2 births | 0.156 | 0.271 | 0.875(0.690;1.109) |
| Marital status (ref Not married) | 1 | ||
| Married | 0.168 | 0.791 | 1.602(0.764;1.477) |
| Current breastfeeding (ref Yes) | 1 | ||
| No | 0.191 | 0 | 4.598(3.160;6.690) |
| Social Characteristics: | |||
| Wealth Quantile (ref poorest) | |||
| Poorer | 0.406 | 0.442 | 0.732(0.330;1.622) |
| Middle | 0.402 | 0.297 | 0.658(0.299;1.446) |
| Richer | 0.397 | 0.297 | 0.661(0.304;1.438) |
| Richest | 0.398 | 0.152 | 0.565(0.259;1.233) |
| Education level (ref none and primary) | 1 | ||
| Secondary and higher | 0.227 | 0.008 | 1.808(1.171;2.791) |
| Mother currently working (ref No) | 1 | ||
| Yes | 0.236 | 0.235 | 1.323(0.833;2.099) |
| Number of children 5 or under (ref Less than 2) | 1 | ||
| More than 2 children | 0.222 | 0 | 2.911(1.867;4.538) |
| Covariates | (95% CI) |
|---|---|
| Residence (Rural) | |
| Urban | 0.27(0.16;0.39) |
| Current breastfeeding (No) | |
| Yes | 0.38(0.17,0.59) |
| Education (Non & Primary) | |
| Secondary & Higher | 0.38(0.26;0.50) |
| Number of children 5 or under (2 or more) | |
| Less than 2 children | 0.38(0.25,0.52) |
4. DISCUSSION
The 2014 Lesotho Demographic and health survey data was used, where the fully Bayesian approach was performed to model the spatial variation of under-five mortality. This study found that the effect of covariates on under-five mortality varied spatially; however, the spatially varying U5M model was significantly different from the stationary one. The major advantage of the spatially varying model is that it can show the effect of each covariate on U5M in each district [12, 22]. Education, type of resident, and the number of under-five children in the household had more effect on U5M in the Butha-buthe district. Mothers with better education are more likely to adopt alternatives in child care and new treatment and do the family planning to avoid more under-five children in the house. They are also more likely to reside in the places that have well equipped medical facilities and good sanitation infrastructure [23, 24]. Breastfeeding had a most significant effect on almost the whole of Lesotho; this might suggest that mothers of under-five children should be encouraged to breastfeed their children through education and awareness sessions. According to World Health Organisation (WHO), breastfeeding for six months is recommended (for HIV mothers) and continue feeding along with complimentary food in connection with antiretroviral therapy is the best way to overcome mother to child infection to HIV. Age at death of an under-five child was found to have a non-linear effect on under-five mortality. The effect if linear from birth until month 20, where it increases towards month 50. Therefore, this study found that higher child death is associated with children whose age is more than 20 months. These studies were also confirmed by Luchemo, OE., 2017 [13], who showed that the likelihood of malaria infection increases with child age.
To our knowledge, this study is the first to do spatial modelling in Lesotho using the newly developed Statistical models which are able to capture data complexity. We assume that the analysis of the present work will be used to public matter policymakers in their effort to mitigate U5M in Lesotho, by allowing them to understand the areas they need to focus on, in order to enhance the planning and evaluation of health policies to prevent the under-five mortality. Studies like [12, 13, 22] support our findings.
CONCLUSION
In this study, we explored the existing statistical models for mapping and modelling as used in the Bayesian framework and determined the distribution of U5M in Lesotho. We used the recently refined Integrated Nested Laplace Approximation (INLA) package that exists in R software. We applied these models to under-five mortality (U5M). These models only catered for areal (lattice) data. Geostatistical and point pattern data were not considered in this research. The data used in this study was taken from Lesotho Demographic and Health Surveillance (LDHS) for 2014. The non-linear effect of age at death of an under-five child was modelled using the random walk of order 2 (RW2), while the spatially structured effects and spatially unstructured effects in the model were modelled using the Gaussian Markov Random Field and a zero-mean Gaussian process, respectively. In this study, we fitted four stationary models and used the best fitting model to estimate the risk pattern of the U5M in Lesotho. We also fitted four models that allow the effects of the covariates to vary spatially by using the conditional autoregressive model, the best model in terms of small is Watanabe-Akaike Information Criterion (WAIC) which was used to map LDHS data for 2014. The spatially varying coefficients models developed in this study are assumed to provide better smoothing than the stationary models because they give a covariate effect on UM5 on each district.
In the future, we can take into account the method of covariate measurement error using Bayesian techniques. This will ensure that all available data is used in mapping and modelling. Since most diseases that contribute to U5M attacks children immunity, then studies on the relationship between resistance to infection and U5M may help in informing strategies of reducing infections and hence mortality. Knowing how the under-five death is affected by different variables together with time and location can help in tracing the trend of U5M and describe spatial distribution over time through spatiotemporal modelling as Luchemo, O. E. 2017 [13] did. He extended the spatially varying coefficient process model by adding the effect of time and apply the model to malaria prevalence data.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


