All published articles of this journal are available on ScienceDirect.
Covid-19 Mortality Rates in Northamptonshire UK: Initial Sub-regional Comparisons and Provisional SEIR model of First Wave Disease Spread
Abstract
We analysed mortality rates in a non-metropolitan UK subregion (Northamptonshire) using statistically-weighted data fitted to the start of the epidemic to quantify SARS-CoV-2 disease fatalities at sub 1,000,000 population levels. Using parameter estimates derived from the recorded mortality data, a numerical (SEIR) model was developed to predict the spread of Covid-19 sub regionally. Model outputs, including analysis of transmission rates and the basic reproduction number, suggest national lockdown flattened the curve and reduced potential deaths by up to 4000 locally. The modelled number of infected and recovered individuals is higher than official estimates, and a revised form of the theoretical critical population fraction requiring immunisation is derived. Combining published (sub-regional) mortality rate data with deterministic models on disease spread has the potential to help public health practitioners refine bespoke mitigation plans guided by local population demographics.
1. INTRODUCTION
Since the global outbreak of SARS-CoV-2 in December 2019, the UK has been one of the hardest-hit nations in terms of reported mortality rates. Lockdown in the UK started on March 24, 2020, several weeks later than elsewhere in mainland Europe. The UK response has been criticised by some for lagging, despite early mortality data from Hubei, China, South Korea and Italy, where enough information had been gathered to model the initial spread of the virus [1-3].
Data on subsequent UK lockdowns are being analysed with details on the effectiveness of Non-Pharmaceutical Interventions (NPIs) still under review. Early indications suggest it is important not to extrapolate from data aggregated at the national level to make local public health interventions, once the virus has taken a steady hold. Given the duration since the first recorded deaths in the UK, the opportunity now presents itself to look more closely at regional and sub-regional trends that impact on location-specific public health mitigations [4].
The aim of this research is to analyse in detail mortality rates due to Covid-19 in a non-metropolitan UK subregion (Northamptonshire) during spring 2020, to understand SARS-CoV-2 disease fatalities at granular (< 1 million) population level. Northamptonshire was chosen as a case study because while largely a rural county, it has significant centres of urban population with mixed ethnicity, typical of English counties more generally. The detailed comparisons made on mortality rates (and place of death) are a useful catalogue in themselves. In addition, they provide robust input for deterministic models seeking to understand how the virus is spread [2]. An update on mortality rates from December 2020 is now also available [5].
This paper comprises two parts: 1. An analysis of publicly available mortality data in Northamptonshire to June 2020, benchmarked nationally and regionally, and 2) a SEIR mathematical model that applies these data to better understand viral spread locally. Our goal is to combine observations with mathematical models to help improve long-term regional planning and prepare for future likely outbreaks of Covid-19.
2. METHODS
Data on age standardised mortality rates (the weighted average of the age-specific mortality rates per 100 000 of the target population), involving Covid-19 from the period March to June 2020, published on July 24 by the ONS for each district and local authority in Northamptonshire, were analysed [6]. The rates between geographical areas were different (p < 0.05) if there was no overlap in the 95% confidence intervals for the comparison areas. All data used in this study are publicly available and licenced for use under ONS Open Access rules. The SEIR model was run using COMSOL v. 5.5 Multiphysics (Finite Element) software, calibrated against weekly ONS death rates by occurrence in Northamptonshire.
3. REGIONAL MORTALITY RATES
3.1. East Midlands
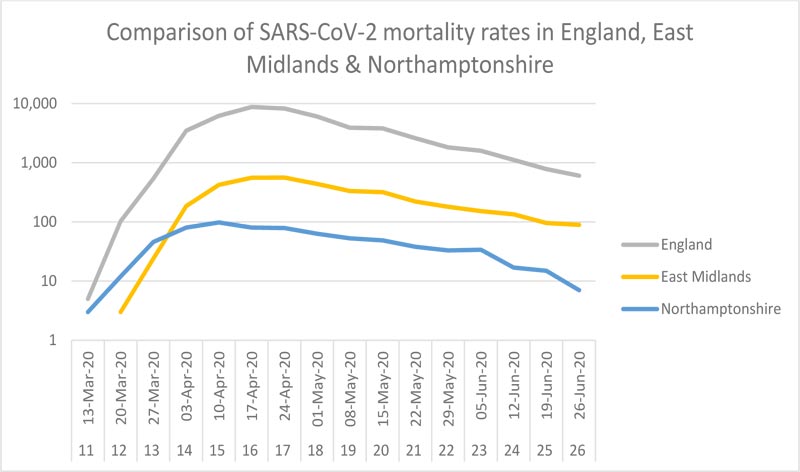
The East Midlands is one of nine official regions of England at the first level of NUTS (The Nomenclature of Territorial Units for Statistics) for statistical purposes. It consists of six English counties, including Northamptonshire, with a combined population of 4.811 million [7]. The largest city by population is Leicester, the site of the first sub-national lockdown in the UK. Northampton is the fourth largest conurbation in the region. A time-series comparison of national to sub-regional mortality rates is shown in Fig. (1).
3.2. Northamptonshire
Northamptonshire (population 753,278 [7], density 316 people/km2) is the southernmost county in the East Midlands region, covering an area of 2,364 km2. The major urban centre is Northampton (population, 224,610) [7]. The 2011 census showed the county to split evenly between males (49.5%) and females (50.5%), with 18.1% of the population aged 65 years and older. Nearly 90% of the population are white (British or other). In terms of governance, Northamptonshire is currently divided into seven boroughs and local district councils following a two-tier structure of local government. In March 2018, new structural changes were proposed that see the existing boroughs and district councils replaced by two unitary authorities of West and North Northamptonshire.
4. ANALYSIS
4.1. Comparison of Age-standardised Covid-19 Death Rates between Northamptonshire Areas
Registered deaths due to Covid-19 in Northamptonshire over the current period of study are 715, comprising approximately 25% of total registered deaths over the same period. The data have been broken down by region and district to allow comparisons. The first recorded Covid-19 death was on March 17 (t = 0, week 11), peaking individually at total of 98 registered deaths in week 15 (April 13-19). Regarding the place of death, the majority (c. 72%) occurred in the hospital. When disaggregated into the seven comprising districts, it becomes clear that Northampton is the dominant contributor to the overall curve profile with the highest Covid-19 mortality rate (Table 1). This is statistically different, at the 5% level, from all other local authority areas except for Corby. South Northamptonshire has the lowest Covid-19 mortality rate, although only the differences with that of Northampton and Kettering are statistically significant. Compared regionally, although Northamptonshire has a statistically significantly higher age-standardised mortality rate than the whole of England, the East Midlands region has a significantly lower rate than England (Fig. 2 and Table 1).

| Area | No. of Deaths | Population Estimates |
Age-standardised Rate (/10,000) |
Lower 95% CI | Upper 95% CI |
|---|---|---|---|---|---|
| Corby | 50 | 72,218 | 101.4 | 74.9 | 134.1 |
| Daventry | 75 | 85,950 | 88.4 | 69.4 | 110.9 |
| E Northamptonshire | 96 | 94,527 | 96 | 77.7 | 117.3 |
| Kettering | 99 | 101,776 | 104.7 | 85.1 | 127.5 |
| Northampton | 269 | 224,610 | 148 | 130.2 | 165.7 |
| S Northamptonshire | 56 | 94,490 | 60.7 | 45.8 | 78.9 |
| Wellingborough | 66 | 79,707 | 87.8 | 67.9 | 111.8 |
| Northamptonshire | 711 | 753,278 | 105 | 97.2 | 112.7 |
| East Midlands | 3812 | 4,835,928 | 79.9 | 77.3 | 82.4 |
| England | 48040 | 56,286,961 | 88.7 | 87.9 | 89.5 |
| Unitary Authority North | 311 | 348,228 | 97.5 | 86.6 | 108.3 |
| Unitary Authority West | 400 | 405,050 | 99.0 | 89.3 | 108.7 |
The new political structure, due to take effect in April 2021, has consequences for the future management and resourcing of public health in its ambition to reduce health inequalities. However, if the new Unitary Authorities were in place, then there would be no statistically significant difference in the Covid-19 mortality rates between them. This is because Northampton, with the highest rate in the county, and South Northamptonshire, with the lowest, are both in the West Northamptonshire Unitary Authority.
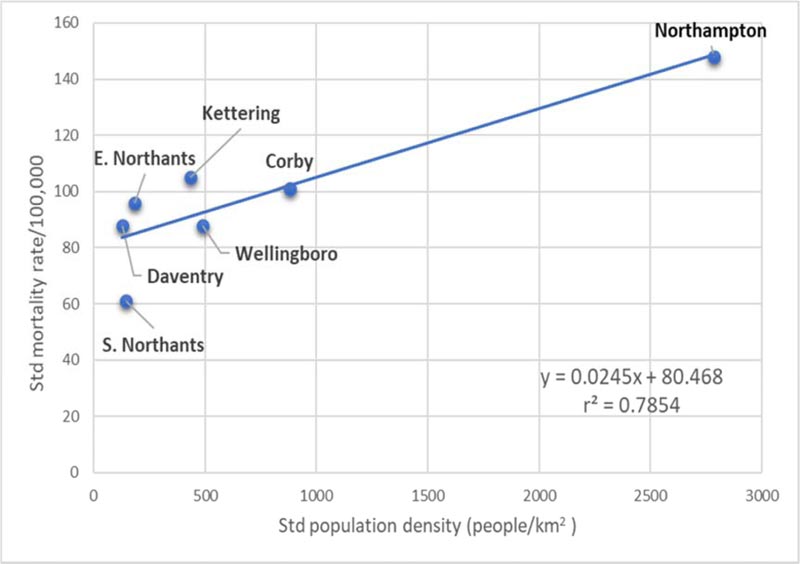
There is also a relationship between the standard population density in each district and the standardised number of fatalities (Fig. 3). This is perhaps not surprising, as people who live closer together stand more chance of transmitting the virus. Northampton has the highest population density per square kilometre in the county and the highest death rate; South Northants has the lowest death rate and second lowest population density. However, we note the standard population density is likely to underestimate the true effect of transmission, which can be improved using the quadratic (population-weighted) density [8].
5. PROVISIONAL SEIR MODEL FOR NORTHAMPTONSHIRE
One of the simplest mathematical techniques used to predict disease transmission is the SEIR model [9, 10], which divides a population N at t = 0 into four ‘compartments’ of susceptible S(t), exposed (meaning infected but not yet infectious) E(t), Infectious, I(t) and recovered R(t). In the model, individuals progress between each compartment at a rate determined by four interlinked ordinary differential equations such that S(t) + E(t) + I(t) + R(t) = N. SEIR models are deterministic (non-probabilistic) and average the infectiousness across a susceptible population. They are thus different from stochastic models where infection is modelled via discrete interactions between individuals [11, 12]. Key variables in both include the transmission rate by infectious individuals (β), the average number of days a person is infectious (n), and the recovery rate γ = 1/n. They are related via: β = R 0/n, where R 0 is the basic reproduction number at t = 0 (defined as R 0 = β/γ). Any mitigation strategy involving NPIs must aim to reduce the reproduction number, for example by decreasing the transmission rate or the time infections individuals are isolated [13].
Current uncertainties in the modelling relate explicitly to the details of disease transmission. Covid-19 is transmitted from symptomatic (infected) people through respiratory droplets or contact with contaminated materials [14]. The infectious period (n) appears maximised in the first three days after infection. The incubation period for Covid-19, which is the time between exposure and symptom onset is 5-6 days on average but can be up to 14 days [15]. During this time (pre-symptomatic) period, an unknown fraction of infected individuals may be contagious, meaning transmission can occur before symptom onset. The model assumes homogenous mixing within the population and does not account for asymptomatic transmission. Imported cases are also excluded, although provision exists to add this variable in future modelling.
6. RESULTS
Two SEIR models are presented. In the ‘no reductions’ scenario, the virus is left to run its course after the first registered deaths at t = 0 for a period of 120 days. The second model (‘with restrictions’ Fig. 4) follows the UK Government response with lockdown mitigations imposed on March 24, seven days later. It mimics the effects of social distancing from t = 7 onwards by reducing the transmission rate and basic reproduction number relative to the ‘no restrictions’ case.
Results are summarised in Table 2. The basic reproduction number (2.95) in the ‘no-reductions’ case lies within the reported range for Covid-19 [16], consistent with the early exponential spread of the virus [9]. The simulations highlight the positive impact of reductions on the mortality rate. Allowed to spread uninhibited, total predicted model deaths exceed 4500 against an actual registered of 715, c. six times higher than currently recorded. In contrast, the ‘with reductions’ scenario, where the transmission rate is reduced by c. 60%, predicts 663 deaths over the same period, fitting closely the actual record (Table 2). The potential number of infected individuals is reflected in the number of recovered (R(t)) cases. The ‘with reductions’ model implies 135,800 discrete exposures to the virus over the simulation period, equating to approximately 18% of the total population. This value is significantly in excess of cases reported for Northamptonshire [17] and is received with caution. It is, however, consistent with evidence for significant underreporting of infections during the initial phase of the pandemic. For example, only around 15% of active cases were registered in Wuhan [18, 19], while SIR modelling by Lourenco et al. [20] suggests the epidemic in the UK started at least a month before the first reported death. If so, that introduces a minimum lag in the Northamptonshire data of t = -78 days, enough in principle to build up a sizeable reservoir of unreported cases. Real-time polymerase chain reaction (RT PCR) testing, now routine in the UK, has revealed at face value a high background prevalence, although there is reason to believe that random mass testing may also overestimate the true incidence rate [21, 22].
| Model Inputs | Symbol/Expression |
SEIR ‘No Reductions’ |
SEIR ‘with Reductions’ |
|---|---|---|---|
| Population | N | 7.533E+05 | 7.533E+05 |
| Infectious at t = 0 | I | 3 | 3 |
| Transmission rate (day-1) | β | 0.98 | 0.40 |
| End of simulation time (days) | t | 120 | 120 |
| Day reductions introduced | - | - | 7 |
| Days infectious | n | 3 | 3 |
| Recovery rate from infection | γ =1/n | 0.33 | 0.33 |
| Total recovered | R(t) | 7.01E+05 | 1.36E+05 |
| Total deaths | D | 4585 | 663 |
| Basic reproduction number | R0 | 2.95 | 1.21 |
| Critical immunisation threshold | ρc | 66% | 14% |

Although the results are provisional and subject to revision as new data emerge (meaning the parameterised fit to the mortality data may change), they nonetheless provide information about disease veracity and spread useful for guiding public health mitigation at the sub-regional level [4].
7. DISCUSSION
7.1. Implications for Herd Immunity and Immunisation
We end with a practical example of how SEIR model outputs may be useful in informing public health interventions locally. The critical vaccination threshold needed to prevent further infection must satisfy the inequality ρ ≥ ρc, where ρc = 1-1/R0 (or interchangeably 1/Re where Re is the effective reproduction number [10],). At the onset of a new infection where there are no prior cases, it is reasonable to assume S(t) ≡ ρ, the proportion that require vaccination. However, the SEIR models reveal a sizeable fraction R(t) of recovered cases. The relevant differential equation is:
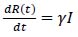 |
(1) |
where, after integration, R(t) = γIt + c, allowing the number of recovered individuals to be simulated over time. If recovery confers immunity to future infection, as is the case normally in communicable disease transmission, it would suggest these individuals could be excluded, reducing the overall size of the susceptible population by R(t)/ρ = φ. In this case, the modified critical fraction of the population requiring early immunisation is:
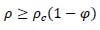 |
(2) |
Applying this criterion, the revised critical fraction could in theory be as low as 14% (Table 2). Other independent estimates support the idea that Covid-19 critical immunisation thresholds may be less than 50% conditional on the time-varying reproduction number [23, 24].
We stress again caution is required in when interpreting SEIR model outputs based on data early in the pandemic. As experience from previous epidemics has shown [10, 13], initial results may require subsequent revision. Future work will seek to incorporate the geographical and demographic variations identified in the statistical analysis (Table 1) to help refine SEIR models that provide deeper understanding of the dynamics of Covid-19 at sub-regional level.
CONCLUSION
Initial results show age-standardised, Northamptonshire mortality rates during spring 2020 from Covid-19 are higher than both regional and national averages. Northampton is the single biggest contributor to mortality rates, with South Northamptonshire the lowest (significance level p = 0.05). This trend follows current known distributions in health inequalities [17]. A SEIR model, calibrated by fitting to mortality rate, yields predictions about the dynamics of virus spread and local impact of reductions in β and R 0. The introduction of NPIs may have resulted in up to 4000 fewer deaths in Northamptonshire. Estimates of recovery rates suggest up to 18% of individuals in the county may have been infected, requiring any future immunisation programme to target only a revised critical maximum fraction of the susceptible population initially to contain the spread
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
All data are anonymous and publicly available under Open License from the UK Office of National Statistics (London).
FUNDING
This research received funding from University of Northampton, reference: OVC 2020.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


