All published articles of this journal are available on ScienceDirect.
Application of Quantile Regression: Modeling Body Mass Index in Ethiopia
Abstract
Background:
Child malnutrition is the leading public health problem in developing countries. It is a major cause of child morbidity and mortality. Under-five children are the most vulnerable group for malnutrition. Body Mass Index (BMI) is a measure of nutritional status and is defined as the ratio of weight (kg) to squared height (m2). Studying the determinants of under-five children’s BMI is an important issue that needs to be addressed. This study applies quantile regression to study the determinants of under-five children BMI in Ethiopia.
Methods:
The weight-for-height index measures BMI. Quantiles are a generalization of percentiles for continuous random variables. Because it makes no distributional assumption about the error term in the model, quantile regression offers considerable model robustness.
Results:
The findings using quantile regression at different quantile levels were presented. The estimates across quantile levels were also performed. The findings of this study identified that for children under the age of five, the current age of mother, mother’s BMI, region (SNNPR and Somali) and weight of the child at birth (average and large) were found to be significantly affecting under-five children’s BMI across quantile levels.
Conclusion:
Quantile regression allows us to study the impact of predictors on different quantiles of the response distribution, and thus provides a complete picture of the relationship between the dependent and explanatory variables.
1. INTRODUCTION
Having healthy individuals in the population equates to the wealth of a country. Nutrition is the vital precondition for good health. Body Mass Index (BMI) is used as a screening tool to indicate whether a person is underweight, overweight, obese or a healthy weight for their height. However, BMI is not a direct measure of body fatness. If a person’s BMI is out of the healthy BMI range the risks of illness or death may increase significantly. For children, BMI is dependent on age and sex and is often referred to as BMI-for-age. A high amount of body fat in persons or children can lead to weight related diseases and other health issues and being underweight can also put one at risk for health issues [1, 2].
The nutrition of infants and young children is triggering great concern in any society. About 45 percent of deaths of children under the age of five are linked to malnutrition [3]. In 2015 more than half of stunted under-five children lived in Asia while more than one-third lived in Africa. Sub-Saharan Africa has one of the highest levels of child malnutrition. In Ethiopia, 29 percent of children under the age of five are underweight, and 9 percent are severely underweight. According to the 2016 EDHS report, overall 38 percent of children under the age of five are stunted, 10 percent are wasted, 24 percent are underweight, and 1 percent are overweight. This indicates that Ethiopia is among those countries with the highest rate of malnutrition in Sub-Saharan Africa.
Globally, an estimated 101 million children under-five year of age, or 16%, were underweight (i.e. weight for age below -2SD) in 2011, a 36 percent decrease from an estimated 159 million in 1990. Although the prevalence of stunting and underweight among children under five years of age has decreased worldwide since 1990, overall progress is insufficient and millions of children remain at risk [4, 5]. Therefore, malnutrition is a considerable health problem that needs due attention because reducing malnutrition in children is equivalent to improving the health status of these children. This is equivalent to improving the health status of future generations of that society and is indispensable for the economic growth and development of the society under consideration.
Children’s BMI under the age of five at or above the 95th percentile, between the 85th and 95th percentile and between the 5th and 85th percentile were classified as obese, overweight and normal (healthy weight) respectively [6]. The cutoff point for underweight of less than the 5th percentile is based on recommendations by the World Health Organization Expert Committee on Physical Status. The percentiles are age-specific for children but not for adults [7].
2. METHODS AND MATERIALS
For this study, the 2016 Ethiopian Demographic and Health Survey was used. The survey was carried out by the Central Statistical Agency of Ethiopia. For the survey 645 clusters, 202 in urban areas and 443 in rural areas, were selected. The survey was conducted in 16650 residential households, 5232 in urban areas and 11418 in rural areas. The sample was expected to generate an estimated 16663 completed interviews with women aged 15-49, 5514 in urban areas and 11149 in rural areas, and 14195 completed interviews with men aged 15-59, with 4472 in urban areas and 9723 in rural areas [8].
2.1. Study Variable
The response variable in this study is under-five children’s BMI, which is a continuous variable. The explanatory variables used in this study are:- child’s age, sex of child, weight of child at birth, mother’s current age, mother’s BMI, educational attainment of mother, mother’s work status, religion, region, wealth index, place of residence (rural or urban), and current marital status. The socio-economic and demographic factors used in this study were supported by several researchers as most likely to be referred to as intermediate variables for the determinants of children’s nutritional status [18].
The main objective of this study is applying quantile regression to identify factors associated with different quantiles of under-five children’s BMI as a function of age and other relevant factors. It will assist policy makers to know and understand the areas they need to focus on in order to enhance the planning and evaluation of health policies to prevent children’s deaths and to enhance children’s health, diet and growth.
2.2. Statistical Methods
Quantiles are a generalization of percentiles for continuous random variables. Quantiles are cut points dividing the range of a probability distribution into contiguous intervals with equal probabilities or dividing the observations in a sample in the same way. In SAS the QUANTREG procedure models the effect of covariates on the conditional quantiles of a response variable by means of quantile regression. Ordinary least squares regression models the relationship between one or more covariates X and the conditional mean of the response variable given X = x or E[Y|X=x]. Quantile regression, which was introduced by Koenker and Bassett in 1978, extends the regression model to conditional quantiles of the response variable, such as 0.25 quantile or 25th percentile, 0.5 quantile or 50th percentile, 0.75 quantile or 75th percentile and so on other than just the conditional mean of the response variable. Quantile regression is desired if conditional quantiles are of interest. It is also particularly useful when the rate of change in the conditional quantile, expressed by the regression coefficients, depends on the quantile [9].
Quantile regression, which includes median regression as a special case, provides a complete picture of the covariate effect when a set of percentiles is modeled. So it can capture important features of the data that might be missed by models that average over the conditional distribution [9-11]. Quantile regression methods are applied to continuous-response data with no zero values and possibly utilize them in the context of count data [12, 13].
Suppose Y is the response variable, and X is the p-dimensional predictor: Let FY(Y/X=x) = P(Y Y/X=x) denote the conditional cumulative distribution function of Y given X=x. Then the τth conditional quantile of Y is defined as:
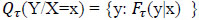 |
(1) |
where the quantile level τ ranges between 0 and 1. In particular, the median is Q1/2.
The quantile regression model is described by the conditional τth quantiles of the response Y for given values of predictors x1,x2,...,xk. It is a natural extension of the traditional mean model in Eq (1):
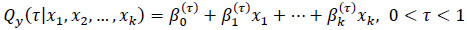 |
(2) |
where 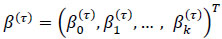 is the unknown parameter vector.
is the unknown parameter vector.
Eq (2) specifies the changes in the conditional quantiles. Since any τth quantile can be used, it is possible to model any predetermined position of the distribution and to achieve a more complete understanding of how the response distribution is affected by the predictors. Thus, it allows us to choose positions on the response distribution for their specific inquiries.
For a random sample {y1,...,yn} of Y, it is well known that the sample median minimizes the sum of absolute deviations Eq. (3).
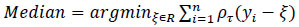 |
(3) |
Likewise, the general τth sample quantile ξ(τ), which is the analogue of Q(τ), is formulated as the minimizer:
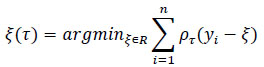 |
where ρτ(Z)=Z(τ-I(Z<0)), 0<τ<1, and where I(·) denotes the indicator function. The loss function ρτ assigns a weight of τ to positive residuals yi-ξ and a weight of 1-τ to negative residuals. Using this loss function, the linear conditional quantile function extends the τth sample quantile ξ(τ) to the regression setting in the same way that the linear conditional mean function extends the sample mean.
OLS regression estimates the linear conditional mean function E(Y|X = x) = x'β, by solving: Eq (4)
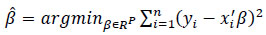 |
(4) |
The estimated parameter 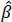 minimizes the sum of squared residuals in the same way that the sample mean
minimizes the sum of squared residuals in the same way that the sample mean 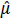 minimizes the sum of squares:
minimizes the sum of squares:
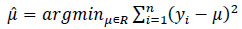 |
Quantile regression also estimates the linear conditional quantile function, (τ|X = x) = x'β(τ), by solving: Eq. (5)
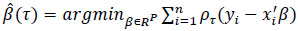 |
(5) |
For any quantile τ (0,1) the quantity
(0,1) the quantity 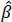 (τ) is called the τth regression quantile. The case τ = 0.5, which minimizes the sum of absolute residuals, corresponds to median regression, which is also known as L1 regression. The set of regression quantiles {β(τ):τ
(τ) is called the τth regression quantile. The case τ = 0.5, which minimizes the sum of absolute residuals, corresponds to median regression, which is also known as L1 regression. The set of regression quantiles {β(τ):τ (0,1)} is referred to as the quantile process.
(0,1)} is referred to as the quantile process.
Quantile regression minimizes: Eq. (6)
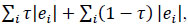 |
(6) |
Where ∑iτ|ei| is a sum that gives the asymmetric penalties τ|ei| for under prediction and (1 - τ)|ei| for over prediction.
The SAS QUANTREG procedure computed the quantile function Q(τ|X = x) and conducts statistical inference on the estimated parameters 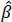 (τ).
(τ).
The τth quantile regression estimator 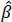 (τ) minimizes over βτ the objective function is: Eq. (7)
(τ) minimizes over βτ the objective function is: Eq. (7)
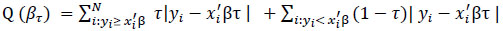 |
(7) |
where 0<τ<1,i:yi≥x'iβ for under prediction, i:yi < x'iβ for under prediction. We have βτ instead of β, because different choices of τ estimates different values of β.
Since the τth conditional quantile of Y given x is given by Qτ(yi|xi) = x'iβτ, its estimate is given by 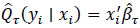 . As one increases τ continuously from 0 to 1, one traces the entire conditional distribution of Y, conditional on x. Note that various quantile regression estimates are correlated. The parameter estimates in quantile regression models have the same interpretation as those of any other linear model as rates of changes. Therefore, in a similar way to the OLS model, the βi(τ) coefficient of the quantile regression model can be interpreted as the rate of change of the τth quantile of the dependent variable distribution per unit change in the value of the ith regressor [14].
. As one increases τ continuously from 0 to 1, one traces the entire conditional distribution of Y, conditional on x. Note that various quantile regression estimates are correlated. The parameter estimates in quantile regression models have the same interpretation as those of any other linear model as rates of changes. Therefore, in a similar way to the OLS model, the βi(τ) coefficient of the quantile regression model can be interpreted as the rate of change of the τth quantile of the dependent variable distribution per unit change in the value of the ith regressor [14].
2.3. Advantages of Quantile Regression
Quantile regression is a useful model if the interest is on conditional quantile functions. The main advantage of quantile regression in comparison to the ordinary least squares regression, is that the estimates of quantile regression are more robust against outliers. Nevertheless, the main use of quantile regression is based on different measures. These measures are central tendency and statistical dispersion and these can be useful to obtain a more all-inclusive analysis of the relationship between variables [10]. Because quantile regression does not assume a particular distribution for the response, nor does it assume a constant variance for the response, unlike ordinary least squares regression, quantile regression offers considerable model robustness. The BMI considered for this study is the continuous outcome. It also allows us to study the impact of predictors on different quantiles of the response distribution, and thus provides a complete picture of the relationship between the dependent and explanatory variables. Quantile regression is also flexible because it does not involve a link function and distributional assumption (such as the normal or poisson distribution) that relates the variance and the mean of the response variable.
Details about quantile regression can be found in various literatures [10, 12, 13, 15-17, 19].
3. RESULTS
The quantile regression model was applied to the 2016 Ethiopian DHS data and the results of the application are discussed herein. SAS QUANTREG procedure was used for model fitting. As shown in Table 1 the median BMI is the same value as the 50th percentile or the second quantile (15.26); children with BMI less than 12.59 (5th percentile) are considered as underweight, children with BMI between 12.59 to 17.02 (5th to 85th percentile) are considered as normal (healthy weight), children with BMI between 17.02 to 18.49 (falls between 85th to 95th percentile) are considered as overweight and children with BMI greater than 18.49 (falls above the 95th percentile) are considered as obese. Moreover, the mother’s mean BMI is found to be 20.72.
| Characteristic | BMI |
|---|---|
| Median | 15.26 |
| 5th percentile | 12.59 |
| 25th percentile, the first quantile (Q1) | 14.19 |
| 50th percentile, the 2nd quantile (Q2) | 15.26 |
| 75th percentile, the third quantile (Q3) | 16.34 |
| 85th percentile | 17.02 |
| 95th percentile | 18.49 |
Table 2 shows that 51% of the children were males and the remaining 49% of the children were females. The majority of the children were from Oromia (15.4%) followed by Somali (13.4%) and SNNPR (12.5%) regions. More than three-fourths of the children live in rural areas (81.9%). About 53.8% of them were from underprivileged (poor) families. 42.1 percent of the children have average weight at birth. Children whose birth weight is less than 2.5 kilograms, or children reported to be “very small” or “smaller than average”, have a higher than average risk of early childhood death [8]. The sample is taken in which the study observes their weight and height measures.
| Characteristic | Description | Total (n) | Percentage |
|---|---|---|---|
| Current age of child | 0 | 1948 | 21.7 |
| 1 | 1798 | 20.0 | |
| 2 | 1738 | 19.4 | |
| 3 | 1695 | 18.9 | |
| 4 | 1792 | 20.0 | |
| Mother’s current age | 15-19 | 320 | 3.5 |
| 20-24 | 1805 | 20.2 | |
| 25-29 | 2695 | 30.0 | |
| 30-34 | 2023 | 22.6 | |
| 35-39 | 1413 | 15.8 | |
| 40-44 | 550 | 6.2 | |
| 45-49 | 165 | 1.8 | |
| Sex of child | Male | 4979 | 51.0 |
| Female | 4793 | 49.0 | |
| Region | Tigray | 940 | 10.50 |
| Afar | 854 | 9.50 | |
| Amhara | 889 | 9.90 | |
| Oromia | 1386 | 15.40 | |
| Somali | 1199 | 13.40 | |
| Benishangul-Gumuz | 727 | 8.10 | |
| SNNPR | 1122 | 12.50 | |
| Gambela | 579 | 6.50 | |
| Harari | 458 | 5.10 | |
| Addis Adaba | 397 | 4.40 | |
| Dire Dawa | 420 | 4.70 | |
| Place of residence | Urban | 1623 | 18.10 |
| Rural | 7348 | 81.90 | |
| Religion | Orthodox | 2702 | 30.10 |
| Catholic | 55 | 0.60 | |
| Protestant | 1610 | 17.90 | |
| Muslin | 4447 | 49.60 | |
| Traditional | 88 | 1.00 | |
| Other | 69 | 0.80 | |
| Wealth index | Poor | 4826 | 53.80 |
| Middle | 1289 | 14.40 | |
| Rich | 2856 | 31.80 | |
| Mother work status | No | 6495 | 72.40 |
| Yes | 2476 | 27.60 | |
| Educational attainment of mother | No education | 5745 | 64.00 |
| Primary school | 2302 | 25.70 | |
| Secondary school | 607 | 6.80 | |
| Higher | 317 | 3.50 | |
| Current marital status | Not married | 572 | 6.40 |
| Married | 8399 | 93.60 | |
| Size of child at birth | Large | 2678 | 29.90 |
| Average | 3781 | 42.10 | |
| Small | 2424 | 27.00 | |
| Don't know | 88 | 0.01 |
3.1. Quantile Regression Analysis
Table 3 shows the estimates and significant effect of the parameters across quantile levels. It was found that current age of mother, mother’s BMI, region (Addis Ababa, SNNPR and Somali), and child size at birth (average and large) were found to have significant effect on under-five children’s BMI at 0.05 quantile. At 0.5 quantile current age of children, current age of mother, mother’s BMI, region (Addis Ababa, Afar, Dire Dawa, Gambela, SNNPR, Somali), place of residence, wealth index (poor and middle) and weight of child at birth (average and large) were found to have significant effect on under-five children’s BMI. Similarly, at 0.85 quantile current age of child, mother’s current age, mother’s BMI, region (Addis Ababa, Dire Dawa, Oromia, SNNPR and Somali) and weight of child at birth (average and large) were found significantly affecting under-five children’s BMI. The findings using quantile regression across quantile levels (0.25 quantile, 0.75 quantile and 0.95 quantile) were also indicated Table 3.
| Parameter | Estimate | p-value | Estimate | p-value | Estimate | p-value | Estimate | p-value | Estimate | p-value | Estimate | p-value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | 10.64 | <.0001 | 13.27 | <.0001 | 14.61 | <.0001 | 15.93 | <.0001 | 16.79 | <.0001 | 18.63 | <.0001 |
| Quantile Level | 0.05 | 0.25 | 0.50 | 0.75 | 0.85 | 0.95 | ||||||
| Current age of children | 0.03 | 0.3486 | -0.19 | <.0001 | -0.29 | <.0001 | -0.38 | <.0001 | -0.44 | <.0001 | -0.64 | <.0001 |
| Current age of mother | 0.00 | 0.7245 | -0.01 | 0.001 | -0.01 | 0.0011 | -0.01 | 0.0055 | -0.01 | 0.0085 | -0.01 | 0.5091 |
| Mother’s BMI | 0.05 | <.0001 | 0.07 | <.0001 | 0.07 | <.0001 | 0.07 | <.0001 | 0.08 | <.0001 | 0.08 | <.0001 |
| Sex of child (Ref. Male) | ||||||||||||
| Female | -0.22 | 0.0036 | -0.22 | <.0001 | -0.20 | <.0001 | -0.24 | <.0001 | -0.22 | <.0001 | -0.25 | 0.0181 |
| Region (Ref. Tigray) | ||||||||||||
| Addis Adaba | 0.66 | 0.0021 | -0.23 | 0.0506 | 0.36 | 0.0021 | 0.22 | 0.2058 | 0.50 | 0.0265 | 0.91 | 0.0059 |
| Afar | 0.28 | 0.1625 | 0.42 | 0.0044 | -0.34 | 0.0005 | -0.46 | 0.0003 | -0.29 | 0.0589 | -0.32 | 0.2562 |
| Amhara | 0.30 | 0.0564 | 0.05 | 0.5783 | -0.02 | 0.782 | -0.15 | 0.0837 | -0.01 | 0.8816 | -0.37 | 0.1181 |
| Benishangul-Gumuz | 0.32 | 0.1145 | 0.07 | 0.467 | -0.09 | 0.3272 | -0.19 | 0.0688 | -0.12 | 0.3425 | -0.10 | 0.7283 |
| Dire Dawa | -0.24 | 0.4795 | -0.15 | 0.3288 | -0.23 | 0.04 | -0.49 | 0.0008 | -0.41 | 0.0055 | -0.18 | 0.5495 |
| Gambela | -0.12 | 0.6427 | -0.07 | 0.5731 | -0.28 | 0.0296 | -0.41 | 0.0044 | -0.24 | 0.1471 | -0.21 | 0.4863 |
| Harari | -0.20 | 0.3795 | -0.04 | 0.7909 | 0.04 | 0.7319 | -0.15 | 0.2674 | 0.02 | 0.9288 | 0.03 | 0.93 |
| Oromia | 0.05 | 0.7724 | 0.09 | 0.3489 | -0.02 | 0.8117 | 0.15 | 0.1865 | 0.31 | 0.0137 | 0.49 | 0.1266 |
| SNNPR | 0.59 | 0.0058 | 0.48 | <.0001 | 0.28 | 0.0019 | 0.28 | 0.0157 | 0.41 | 0.0011 | 0.78 | 0.0334 |
| Somali | -0.38 | 0.0315 | -0.72 | <.0001 | -0.81 | <.0001 | -0.86 | <.0001 | -0.77 | <.0001 | -0.92 | 0.0015 |
| Place of residence (Ref. Urban) | ||||||||||||
| Rural | 0.03 | 0.8509 | 0.14 | 0.039 | 0.17 | 0.0195 | -0.06 | 0.4937 | -0.02 | 0.765 | 0.14 | 0.4907 |
| Religion (Ref. Traditional) | ||||||||||||
| Orthodox | 1.16 | 0.0868 | 0.31 | 0.1208 | 0.09 | 0.5961 | 0.04 | 0.887 | -0.39 | 0.2778 | -0.73 | 0.4635 |
| Catholic | 1.09 | 0.2477 | -0.24 | 0.414 | -0.34 | 0.26 | -0.15 | 0.7703 | -0.23 | 0.7783 | -0.12 | 0.9603 |
| Protestant | 0.97 | 0.1664 | 0.20 | 0.2901 | 0.09 | 0.5735 | 0.13 | 0.6383 | -0.33 | 0.3486 | -0.97 | 0.3255 |
| Muslin | 0.92 | 0.1764 | 0.30 | 0.1066 | 0.09 | 0.5557 | 0.05 | 0.8561 | -0.39 | 0.2828 | -0.78 | 0.4273 |
| Other | -0.05 | 0.9719 | 0.26 | 0.3368 | 0.13 | 0.6488 | 0.05 | 0.9195 | -0.17 | 0.7622 | 0.01 | 0.9959 |
| Wealth index (Ref. Rich) | ||||||||||||
| Poor | -0.08 | 0.5335 | -0.12 | 0.0238 | -0.13 | 0.0179 | -0.12 | 0.0925 | -0.14 | 0.0708 | -0.23 | 0.1637 |
| Middle | 0.08 | 0.603 | -0.11 | 0.1052 | -0.13 | 0.0244 | -0.22 | 0.0089 | -0.13 | 0.167 | -0.39 | 0.0302 |
| Work Status (Ref. Yes) | ||||||||||||
| No | -0.01 | 0.9022 | -0.06 | 0.1818 | -0.03 | 0.4848 | -0.01 | 0.7833 | -0.04 | 0.4524 | -0.05 | 0.7069 |
| Educational level (Ref. Secondary) | ||||||||||||
| No education | -0.32 | 0.0997 | -0.11 | 0.2353 | 0.00 | 0.9731 | 0.04 | 0.698 | 0.04 | 0.7498 | 0.03 | 0.9073 |
| Primary | -0.09 | 0.6136 | -0.06 | 0.4997 | -0.01 | 0.9075 | 0.02 | 0.8119 | -0.01 | 0.9432 | -0.13 | 0.6425 |
| Higher | -0.35 | 0.182 | 0.05 | 0.7099 | 0.17 | 0.1533 | 0.23 | 0.1473 | 0.16 | 0.3296 | -0.15 | 0.6936 |
| Marital status (Ref. Not married) | ||||||||||||
| Married | 0.03 | 0.8503 | -0.02 | 0.8395 | -0.10 | 0.2176 | 0.04 | 0.6952 | 0.06 | 0.564 | 0.02 | 0.9404 |
| Weight of child at birth (Ref. Small) | ||||||||||||
| Average | 0.46 | <.0001 | 0.26 | <.0001 | 0.24 | <.0001 | 0.32 | <.0001 | 0.30 | <.0001 | 0.37 | 0.0055 |
| Large | 0.60 | <.0001 | 0.40 | <.0001 | 0.43 | <.0001 | 0.46 | <.0001 | 0.42 | <.0001 | 0.44 | 0.0017 |
| Don't know | -0.17 | 0.8959 | -0.34 | 0.2375 | -0.11 | 0.6086 | -0.24 | 0.3628 | -0.15 | 0.6844 | 0.14 | 0.7656 |
At 0.25 quantile, intercept = 13.27, which is the predicted value of the 0.25 quantile under-five children BMI when all the explanatory variables are zero. 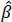 1(0.25 quantile) = -0.19 indicates the rate of change of the 0.25 quantile (Q1) of the dependent variable distribution per unit change in the value of the first regressor (current age of child), keeping all the other explanatory variables constant. In other words, the Q1 regression coefficient indicates that 25% of the under-five children’s BMI will decrease by -0.19 for every one unit change in current age of a child, setting all the other explanatory variables constant. Q1 is a value that has 25% of the observations smaller or equal to it.
1(0.25 quantile) = -0.19 indicates the rate of change of the 0.25 quantile (Q1) of the dependent variable distribution per unit change in the value of the first regressor (current age of child), keeping all the other explanatory variables constant. In other words, the Q1 regression coefficient indicates that 25% of the under-five children’s BMI will decrease by -0.19 for every one unit change in current age of a child, setting all the other explanatory variables constant. Q1 is a value that has 25% of the observations smaller or equal to it.
At 0.5 quantile, intercept = 14.61, which is the predicted value of the 0.5 quantile under-five children’s BMI when all the explanatory variables are zero. 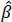 3(0.25 quantile) = 0.07 indicates the rate of change of the 0.5 quantile (Q2) of the dependent variable distribution per unit change in the value of the third regressor (mother’s BMI), keeping all the other explanatory variables constant. In other words, the Q2 regression coefficient indicates that 50% of the under-five children’s BMI will increase by 0.07 for every one-unit change in mother’s BMI, setting all the other explanatory variables constant. Q2 is a value that has 50% of the observations smaller or equal to it.
3(0.25 quantile) = 0.07 indicates the rate of change of the 0.5 quantile (Q2) of the dependent variable distribution per unit change in the value of the third regressor (mother’s BMI), keeping all the other explanatory variables constant. In other words, the Q2 regression coefficient indicates that 50% of the under-five children’s BMI will increase by 0.07 for every one-unit change in mother’s BMI, setting all the other explanatory variables constant. Q2 is a value that has 50% of the observations smaller or equal to it.
At 0.75 quantile, intercept = 15.93, which is the predicted value of the 0.75 quantile of under-five children’s BMI when all the explanatory variables are zero. 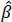 2(0.75 quantile) = -0.01 indicates the rate of change of the 0.75 quantile (Q3) of the dependent variable distribution per unit change in the value of the second regressor (current age of mother), keeping all the other explanatory variables constant. In other words, the Q3 regression coefficient indicates that 75% of the under-five children BMI will decrease by -0.01 for every one unit change in current age of mother, setting all the other explanatory variables constant. Q3 is a value that has 75% of the observations smaller or equal to it; in other words, 25% of the observations are greater than it.
2(0.75 quantile) = -0.01 indicates the rate of change of the 0.75 quantile (Q3) of the dependent variable distribution per unit change in the value of the second regressor (current age of mother), keeping all the other explanatory variables constant. In other words, the Q3 regression coefficient indicates that 75% of the under-five children BMI will decrease by -0.01 for every one unit change in current age of mother, setting all the other explanatory variables constant. Q3 is a value that has 75% of the observations smaller or equal to it; in other words, 25% of the observations are greater than it.
The rate of change of the coefficients across quantile levels for other significant predictors can be interpreted in the same way as above.
3.2. Graphical Assessment of the Explanatory Variables
Figs. (1 to 5) present a concise summary of the quantile regression results of the study variables. Each plot depicts one coefficient in the quantile regression model, the shaded area depicting a 95% pointwise confidence band. In the first panel of the Figure, the intercept of the model may be interpreted as the estimated conditional quantile function of the under-five children BMI across quantile levels. It has a positive effect in the upper quantiles rather than the lower quantiles; the graph indicates a positively upward sloped line across the quantiles. The second plot shows that the effect of current age of child on under-five children’s BMI has a negative effect, especially in the upper rather than the lower quantiles. The third plot shows the effect of mother’s current age in the model. The plot shows a negative effect across quantile levels. The fourth plot shows that the effect of mother’s BMI in the model has a positive effect in the upper quantiles; the graph indicates a positively upward sloped line across the quantiles.
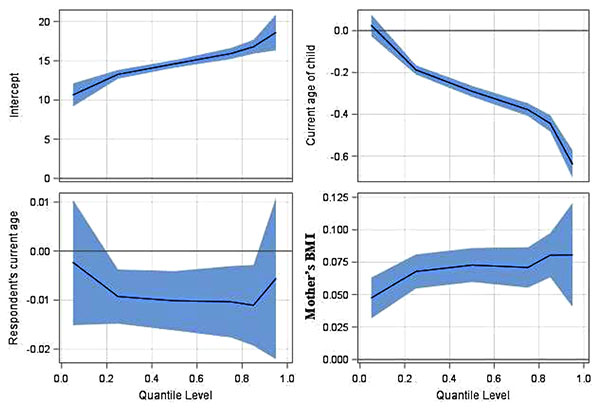
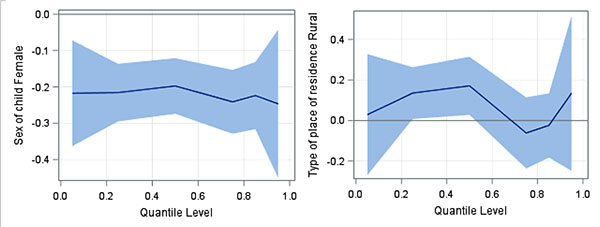
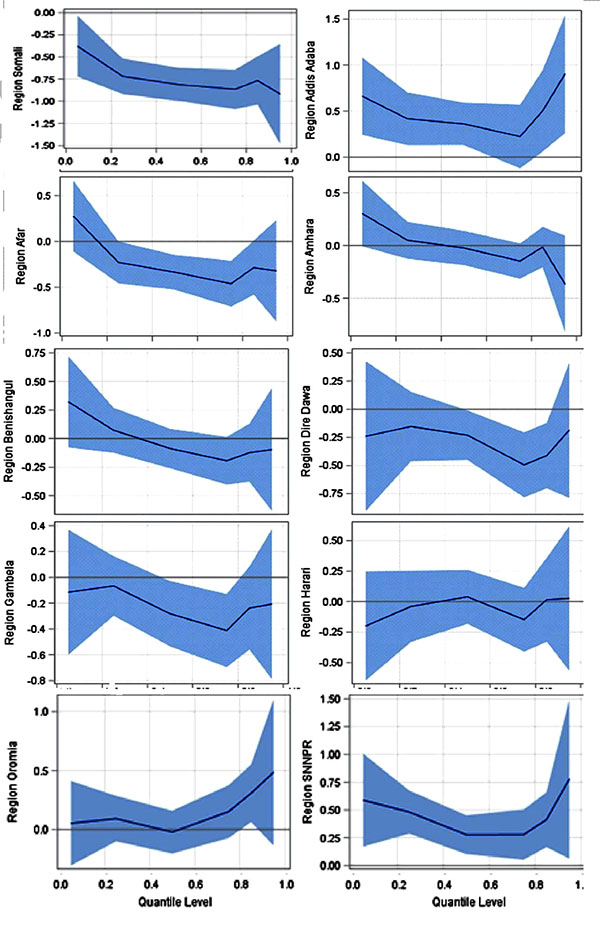
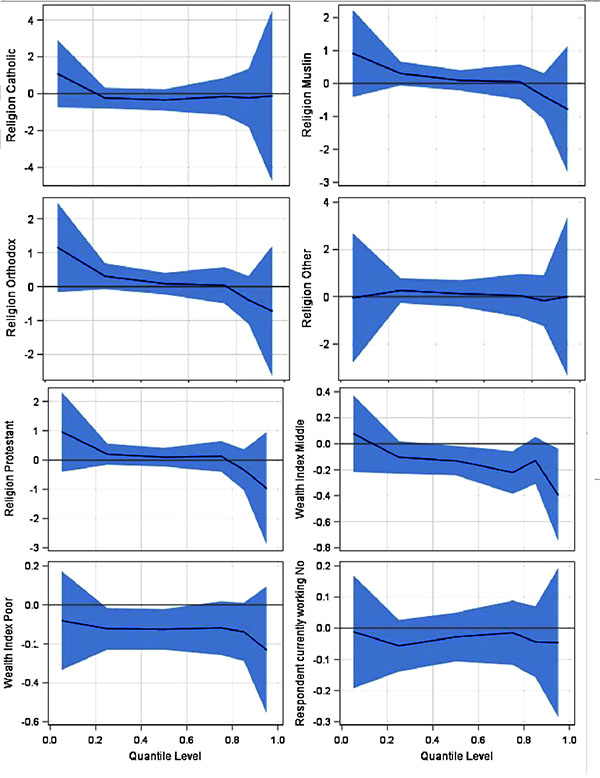

The effect of female child compared to male in the model has a negative effect across the quantiles. Type of place of residence has a positive effect in the middle quantiles. Quantile plot related to region, wealth index, working status, wealth index, religion and weight of child at birth were also presented in Fig. (1-5). The values on the Y-axis in each graph indicate the estimated value of the variables across quantiles levels.
4. DISCUSSION
This paper used quantile regression for the analysis of under-five children’s BMI using the 2016 Ethiopian Demographic and Health Survey. The estimates across quantile levels allow us to study the impact of predictors on different quantiles of the response variable, and thus provide a complete picture of the relationship between the dependent and independent variables. It has also been observed that children under the age of five (except at 0.05 quantile), current age of mother (except at 0.05 and 0.95 quantile), mother’s BMI, region (SNNPR and Somali) and weight of child at birth (average and large) were found to be important variables significantly affecting under-five children’s BMI at all quantile levels.
CONCLUSION
The findings of this study indicate that studying BMI is still an important issue among children under five years of age in Ethiopia. In addition, the findings of the study show that not only education but also environmental and socio-economic factors were found to have significant effects on under-five children’s BMI. Improving the nutritional status of mothers will consequently improve the nutritional status of their children. Policy makers need to focus on the influence of significant factors across all quantile levels to develop strategies of enhancing normal or healthy weight status of under-five children in Ethiopia.
LIST OF ABBREVIATIONS
| BMI | Body Mass Index |
| CDC | Centers for Disease Control and Prevention |
| DFID | The United Kingdom Department for Development |
| EDHS | Ethiopian Demographic and Health Survey |
| UNFPA | The United Nations Population Fund |
| UNICEF | The United Nations Children’s Fund |
| USAID | United States Agency for International Development |
AUTHORS CONTRIBUTIONS
AAY acquired the data, performed the analysis, and drafted the manuscript. AAY, DGA and SM designed the research problem. All authors discussed the results and implications and commented on the manuscript at all stages. All authors contributed extensively to the work presented in this paper. All authors read and approved the final manuscript.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Ethical clearance for the survey was provided by the EHNRI Review Board, the National Research Ethics Review Committee (NRERC) at the Ministry of Science and Technology, the Institutional Review Board of ICF International, and the CDC. Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
COMPETING INTERESTS
The authors declare no conflict of interest, financial or otherwise.
AVAILABILITY OF DATA AND MATERIAL
The data used for this study can be obtained by requesting the ORC macro and DHS.
FUNDING
This work was supported through the DELTAS Africa Initiative. The DELTAS Africa Initiative is an independent funding scheme of the African Academy of Sciences (AAS)’s Alliance for Accelerating Excellence in Science in Africa (AESA) and is supported by the New Partnership for Africa’s Development Planning and Coordinating Agency (NEPAD Agency) with funding from the Welcome Trust [grant 107754/Z/15/Z- DELTAS Africa Sub-Saharan Africa Consortium for Advanced Biostatistics (SSACAB) programmer] and the UK government. The views expressed in this publication are those of the author(s) and not necessarily those of AAS, NEPAD Agency, Welcome Trust or the UK government.
ACKNOWLEDGEMENTS
We thank, with deep appreciation, ORC Macro and Measure DHS for giving us access to the data file.


